2015-08-21
288
Для упрощения исследования преобразования входного сигнала в выходной, входной сигнал разделяется на сумму простых слагаемых. И каждое слагаемое находится по отдельности, а затем все значения складываются, т.к. система линейная.
Гармоника: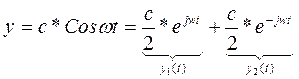 
Пусть y=y1
Найдем частное решение: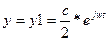 
, предположим, что соответствующее решение имеет вид: x=x1=W(jw)*y1(t)=c/2*W(jw)*ejwt
Подставим x и y в уравнение (1):
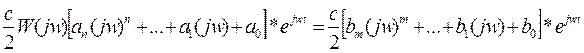(2)
отсюда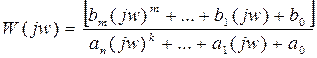 
частотная характеристика системы (1).
Функция комплексная, функция частоты. Соотв. y отличается от входа только коэффициентом. Входной сигнал преобразуется в выходной умножением на множитель jw*ejw
Коэффициент усиления – комплексное число. Коэффициент не зависит от времени, а зависит от частоты w.
Аналогия с комплексными числами- комплексный коэф. усиления.
Любое комплексное число можно представить в виде действительной и мнимой части:
P(w) – действ частотная характериктика (чх)
Q(w) – мнимая чх
A(w) – амплитудная чх
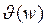- фазовая чх
W(j w)=P(w)+jQ(w)=A(w)*ej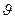 
( w )
w – частотная характеристика.
Связь между характеристиками:
|
|
|
; 
; 
; 
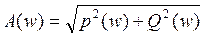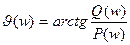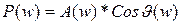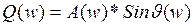
Пусть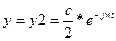 
, тогда y2 отличается от у1, тем что частота отрицательная
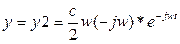
Если x=x1+x2 =c*Cos wt
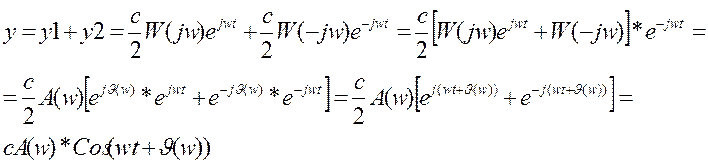
При входном сигнале:
y(t)=c*Cos wt
x(t)=cA(w)*Cos(wt+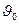 
)
Выходной сигнал – результат преобразования гармоник.
Прохождение гармоник через линейную систему, ее амплитуда С увеличивается в a(w) раз, а фаза на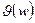 
.
Любой сигнал (периодический) раскладывается в ряд Фурье и его можно представить в виде гармоник.
Преобразование Фурье – обобщение понятия ряда Фурье.
Преобразование Фурье обозначается X(jw),
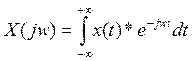
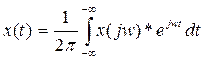
Набор коэффициентов называется СПЕКТРОМ.
