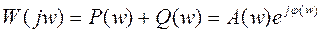Амплитудно и фазочастотные характеристики (годограф Найквиста)

, A(w)—амплитудная хар-ка, 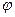(w)—частотная хар-ка.

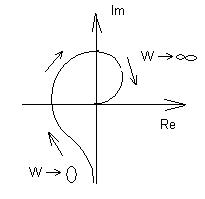
На комплексной плоскости можно изобразить частотную характеристику. При любом значении частота W(jw) представляется вектором на комплексной плоскости. Если изм. частоту от 0 до 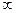, то этот вектор поворачивается и описывает кривую, наз. годографом.

Для статических систем:

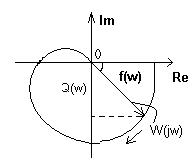
При 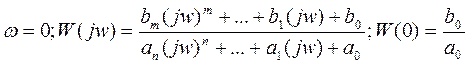--действительное число не равно 0, поэтому годограф выходит с т.А При w→ 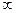в физич-их системах (n>m) W→0. След-но годограф приходит в т.0

Для астатических систем: 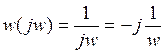. При w→0, W→ .

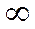12.Логарифмические характеристики (диграмма Боде):

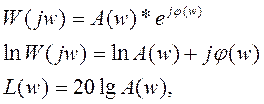
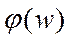- эти две характеристики построены в логарифмическом масштабе частот, наз. логарифмическ. амплитудно- частотной и фазочастотной характеристиками (диаграмма Боде).

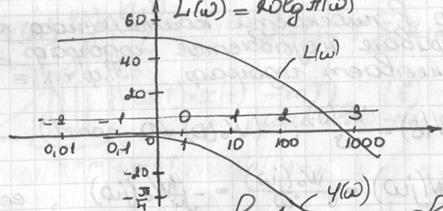
Изменение частоты в 2 раза называется изменением частоты на октаву, а в 10 раз – на декаду: lg(2w)-lg(w) = lg2

lg(10w)-lg(w)=lg10=1

lg10 – децибел

1. Логарифмические характеристики послед. соед. складываются.

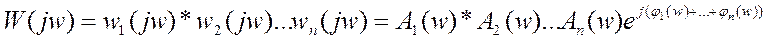
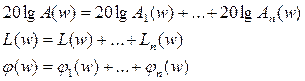
2. Во многих случаях логарифмические амплитудные хар-ки могут быть заменены асимптотическими, т.е. отрезками прямых.