
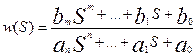 ;
; 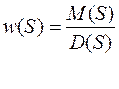
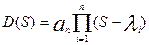
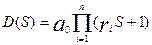
Если среди n корней есть 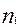 действительных корней и
действительных корней и 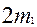 -комплексно сопряженных,
-комплексно сопряженных,
причем 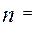
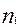 +
+ 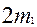 , тогда
, тогда 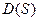 можно представить в виде:
можно представить в виде:
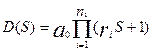
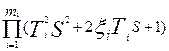

w(S)= 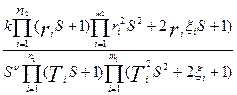
n= 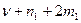
Таким образом передаточную функцию можно представить как последовательное соединение некоторых типовых звеньев (b звеньев):
1.Усилительное звено: w(S)=K
2.Апериодическое звено: w(S)= 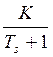
3. Колебательное звено: w(S)= 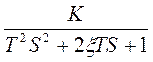
4.Чисто интегрирующее звено: w(S)= 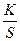
5. Чисто дифференцирующее звено:w(S)=K*S
6. Дифференцирующее звено 1-го порядка: w(S)= 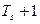
7.Дифференцирующее звено 2-го порядка: w(S)= 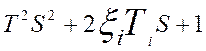
8. Звеночистого запаздывания: w(S)= 
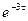
Рассмотрим усилительное звено (идеальное интегрирующее звено): w(S)=K
K(t)=k 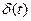 , h(t)=
, h(t)= 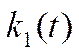
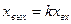 , w(iw)=k=k
, w(iw)=k=k 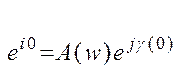
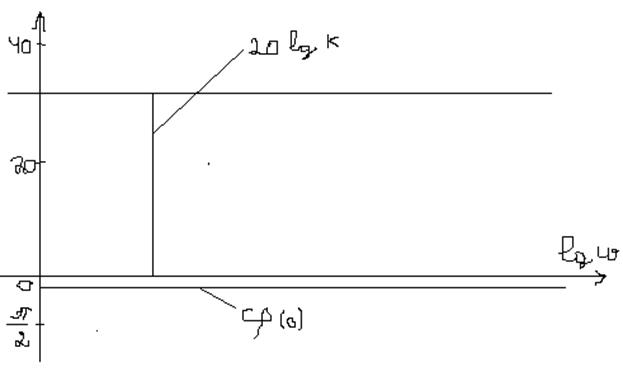
14. Апериодическое звено:
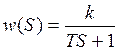
Дифференциальное уравнение, которое описывает это звено.
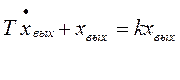 (1)
(1)
Частотные характеристики:

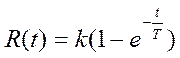 (2)
(2)
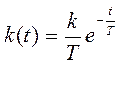 (3)
(3)
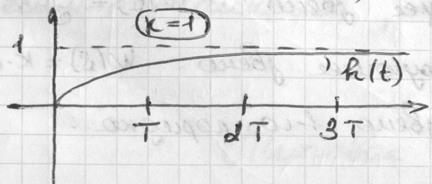
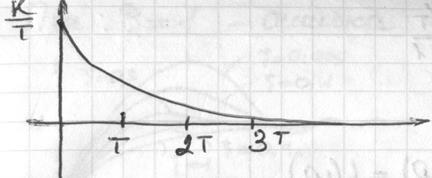
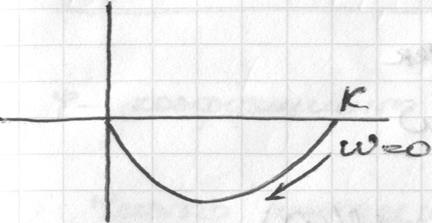
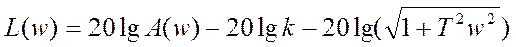
Низкочастотные 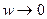 ; при таком w, что
; при таком w, что
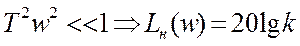
Высокочастотные 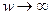 ; при
; при 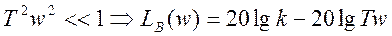
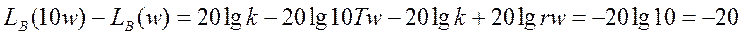
 2015-08-21
2015-08-21 468
468








