2015-08-21
362
Определение – описание системы по данным.
Идентификация – описание системы, определяеться описанием передаточной ф-ции линейной системы по данным о вх и вых сигналах.
Синтез – синтезирование системы по каким-либо данным, что система обеспечивает требуемый показатель качества
Анализ- определение вх по вых сигнала и наоборот.
Идентификация: по экспериментальным данным о вх и вых сигналах можно создать такую мат. модель, которая выполняла бы преобразования вх в вых сигнал.
ИМФ – можно представить как реакцию на единичный импульс.
Технологические процессы изучаються в нормальных условиях(реальная эксплуатация), благодаря подачам пробных сигналов.
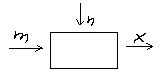m- вх, n-помеха, x-вых
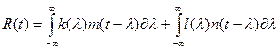
1 часть формулы – связь между вх и вых сигналами во временной области
2 часть формулы – воздействие помех
(формула с учетом воздействия помех)
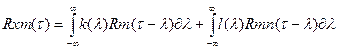
2 часть формулы выражение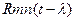 
=0
Если полученный сигнал и помеха не коррелированны, то взаимная коррелированная ф-ия=0
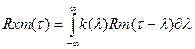(2)
Интеграл свертки имеет вид
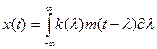
Предположим, что на вх действует белый шум: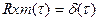 
Тогда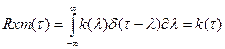 
Если на вх действует сигнал близкий к белому шуму то взаимно корреляционная функция между вх и вых близка к импульсно переходной функции.
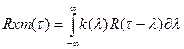
белый шум – асбтрактное понятие которое часто используеться. Его спектральная плотность не зависит от частоты. Дисперсия белого шума =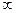 
Термин красный шум существует для отличия одного б.ш от другого.
Решение уравнения методом прямоугольников:
Заменить непрер. Фу-цию ступенчатой (разбить время на интервалы)
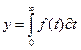
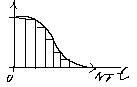
Вместо знач. функции подставить среднее значение (крайнее левое, крайнее правое)
Разобьем весь интервал на несколько подинтервалов. Тогда
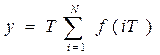
Нижний предел можно положить равным нулю в (1). Нужно учесть все возможные значения k(t)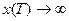 
( импульсная переходная функция)
Тогда по методу прямоугольников получим:
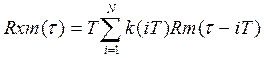
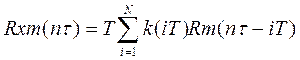(2)
(2)=> 
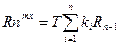(3)
после дискретизации уравнение стало линейным.
Подставим n=1:
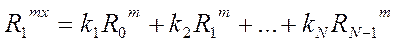
Корреляционная функция четная можно отбросить отрицательность.
Подставим n=e:
…
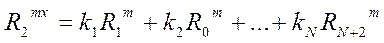
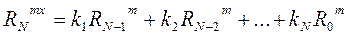
Есть N уравнений(линейн), относительно N-неизвестных
Здесь неизвестно значение импульсной переходной функции. Для очевидности запишем её в матричном виде:
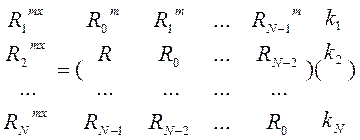
Матрица симметрична
Примерно такой же прием может быть применим для детерминированной функции.
