Монотонный процесс
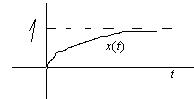
| Время переходного процесса
|
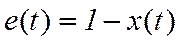
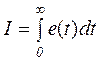 ( I – интегральный показатель )
( I – интегральный показатель )
чем меньше I, тем меньше время переходного процесса
Вычислить интеграл проще, чем найти е, а потом t, что бы при таком t было меньше наперёд заданного значения. 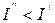
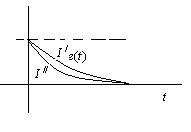
Для немонотонного (колебательного) процесса
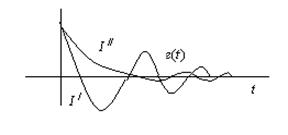
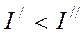 (знаки площадей учитываются при интегрировании)
(знаки площадей учитываются при интегрировании) 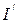 - хуже
- хуже
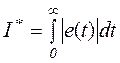 - не будет компенсации за счёт знаков площадей
- не будет компенсации за счёт знаков площадей
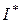 передаёт качество: чем он меньше, тем процесс лучше
передаёт качество: чем он меньше, тем процесс лучше
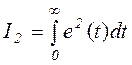 - квадратичный показатель качества, компенсации знаков площадей нет
- квадратичный показатель качества, компенсации знаков площадей нет
чем меньше 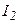 , тем лучше переходный процесс.
, тем лучше переходный процесс.
Вычислить 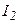 проще, чем сам сигнал ошибки. Минимизация среднего квадрата ошибки (взятие интеграла) общий случай (интеграл от квадрата производной ошибки)
проще, чем сам сигнал ошибки. Минимизация среднего квадрата ошибки (взятие интеграла) общий случай (интеграл от квадрата производной ошибки)
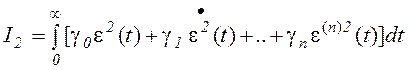
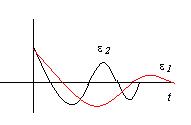
| 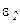 по скорости хуже, по скорости хуже, 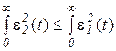 лучше лучше 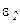
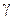 - весовые коэффициенты
отклонение по скорости и отклонения по положению сравниваются (вес каждой ошибки - весовые коэффициенты
отклонение по скорости и отклонения по положению сравниваются (вес каждой ошибки 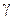 выбирается из анализа сравнения) выбирается из анализа сравнения)
|
26. Определение дисперсии ошибки системы при случайном воздействии
Стационарный процесс – процесс, в котором статические характеристики не зависят от времени.
Характеристики для такого процесса:
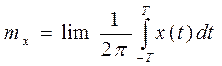 - математическое ожидание
- математическое ожидание
(1) 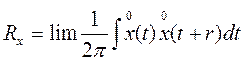 - корреляционный момент
- корреляционный момент
где 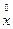 = x – mx => x=
= x – mx => x= 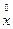 + mx
+ mx
(2) 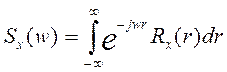 - спектральная плотность
- спектральная плотность
(3) 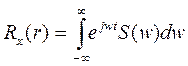
(4) 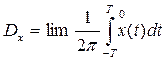 - дисперсии
- дисперсии
(5) Rx (0) = Dx
Из выражения (3) => 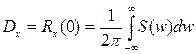 (6)
(6)
Связь между корреляционными функциями на входе и выходе системы.
Пусть x(t)= 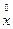 , т.е. mx=0 (для простоты), т.е. будем считать, что процесс уже центрированный.
, т.е. mx=0 (для простоты), т.е. будем считать, что процесс уже центрированный.
Связь между входом и выходом во временной области:
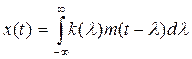
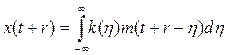
Подставим эти выражения в выражение (1), получим:
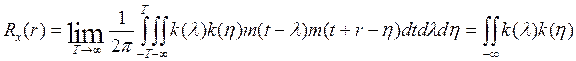
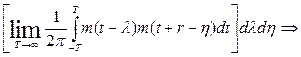
{ […..] – корреляционная функция выходного сигнала}
(7) 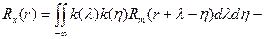 искомая связь.
искомая связь.
Связь между спектральными плотностями
Подставим выражение (7) в (2).
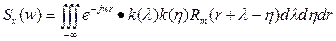 - спектральная плотность выходного сигнала.
- спектральная плотность выходного сигнала.
Преобразуем:
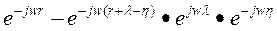
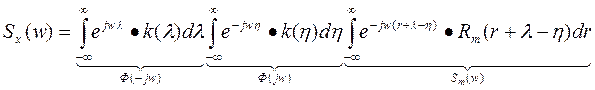 ;
;
{d (r+ λ - η) = dr}
(8) 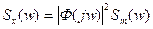 - искомая связь между спектральными плотностями.
- искомая связь между спектральными плотностями.
Спектральная плотность сигнала ошибки:
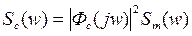
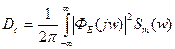
Эти 2 уравнения – определение дисперсии ошибки.
Белый шум – это такой переходный процесс, в котором его корреляционная функция равна дельта функции, а спектральная плотность постоянна во всем диапазоне (в определенном) частот.
Если входной процесс – белый шум, то Sm (w)=c=1, тогда спектральная плотность выходного сигнала численно равна:
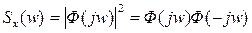
Любую спектральную плотность можно представить как плотность формирующую фильтра.
Говорят, что спектральную плотность можно представить в идее 2-ух комплексно-сопряженных сомножителя, т.е.
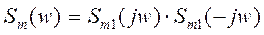
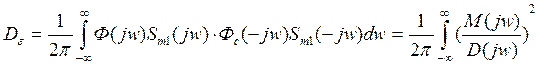
{ 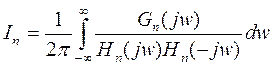
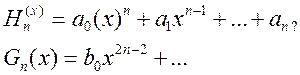
где Все корни H(jw) лежат в верхней полуплоскости}
{……} – табличные выкладки.
 2015-08-21
2015-08-21 404
404








