Аффинное пространство. Координаты точки

Пусть имеется линейное пространство V и множество U элементов произвольной природы, называемых точками и обозначаемых прописными латинскими буквами, причем каждой упорядоченной паре точек М и N поставлен в соответствие единственный вектор x 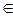V. При этом будем писать x = MN. Предполагается, что соответствие между точками и векторами удовлетворяет аксиомам:

1°. Для каждой точки М 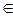U и любого вектора x 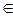V существует единственная точка N 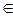U, такая, что МN = x.

2°. Для любых трех точек М, N, Р 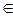U справедливо соотношение

MN + NP = MP.

3°. Для точек М, N 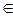U справедливо соотношение MN = 0 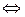М = N (точки совпадают).

Определение 9.9. Множество U, удовлетворяющее аксиомам 1°–3°, называется аффинным пространством, связанным с линейным пространством V.

Аффинное пространство называется n-мерным, если n-мерно соответствующее ему линейное пространство.

Теоремa 9.4. Для любой точки М 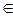U справедливо соотношение ММ = 0. Для любых двух точек М, N 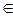U справедливо соотношение MN = – NM.

Доказательство. Из аксиомы 2° при N = М и Р = N следует 2 ММ = = ММ 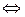ММ = 0. Далее, из этой же аксиомы при Р = М получим MN + NM = = ММ = 0 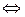MN = – NM. ¨

Пусть U – аффинное пространство. Выберем в нем какую-нибудь точку O и назовем ее началом координат. Тогда для любого вектора x 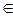V в силу аксиомы 1° найдется единственная точка М, такая, что OМ = x. Тем самым устанавливается взаимно однозначное соответствие между всеми точками М из U и векторами ОМ = x 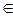V. Вектор ОМ 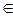V называется радиус-вектором точки М 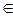U.

Пусть е ^l, е ²,..., е ⁿ – некоторый базис пространства V и вектор x = ОМ имеет в этом базисе координаты x ₁, x ₂,…, x_n. Эти же координаты припишем и соответствующей вектору x точке М, и будем обозначать М (x ₁, x ₂,…, x_n).

Итак, каждой точке n -мерного аффинного пространства в заданном базисе однозначно соответствует совокупность n чисел x ₁, x ₂,…, x_n, называемых ее координатами.

Если М (x ₁, x ₂,…, x_n) и N (y ₁, y ₂,…, y_n) – две точки аффинного пространства U, то в силу аксиомы 2° и формул (8.6) имеем

ОМ + MN = ON 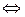MN = ON – ОМ = (y ₁– x ₁) е ^l + (y ₂ – x ₂) е ²+... + (y_n – x_n) е ⁿ,

т. е. координаты вектора MN равны разностям соответствующих координат его конца N и начала М. Тогда согласно формуле (8.7) имеем

MN = (y ₁ – x ₁, y ₂ – x ₂,..., y_n – x_n). (9.9)

Заметим, что если векторы пространства V назвать точками пространства U и каждой упорядоченной паре точек x и у из V поставить в соответствие вектор y – x, то, очевидно, линейное пространство V можно рассматривать как аффинное.

Определение 9.10. Расстоянием 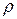(М, N) между двумя точками М и N аффинного пространства называется длина вектора MN, т. е. 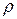(М, N) = || MN ||.

В силу формул (9.4) и (9.9) имеем

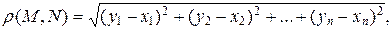
что для точек x и y евклидова пространства R ⁿ совпадает с формулой (9.7).

§9.8. Прямая и гиперплоскость в R ⁿ

Определение 9.11. Будем говорить, что векторы a и b параллельны, если угол между ними равен 0 или p.

Пусть a = (a ₁, a ₂,…, a_n) и b = (b ₁, b ₂,…, b_n). Тогда, как и в случае пространства R ³, легко получить, что

a || b Û ,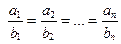

т. е. два вектора a и b в пространстве R ⁿ параллельны тогда и только тогда, когда их координаты пропорциональны.

Пусть a = (a ₁, a ₂,…, a_n) – вектор в R ⁿ, а M ₀ 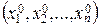– некоторая точка в соответствующем аффинном пространстве R ⁿ. Для любого t 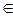R вектор t a параллелен a. В силу аксиомы 1° аффинного пространства найдется единственная точка М (x ₁, x ₂,…, x_n), такая, что M ₀ M = t a. Это соотношение называется векторным параметрическим уравнением прямой в пространстве R ⁿ, которое в координатной форме запишется следующим образом:

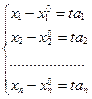Û 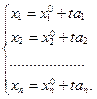(9.10)

Исключив параметр t из системы уравнений (9.10), получим канонические уравнения прямой в пространстве R ⁿ:

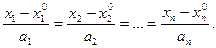
Определение 9.12. Совокупность всех векторов, проходящих через точку M ₀, ортогональных вектору a, называется гиперплоскостью Н в R ⁿ (плоскостью при n = 3).

Пусть c – произвольный вектор, ортогональный a. По аксиоме 1° аффинного пространства существует единственная точка N, такая, что c = M ₀ N. Из условия ортогональности получаем

a 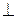c Û (a, M ₀ N) = 0 Û (a, x – x ⁰) = 0,

где x и x ⁰ – радиус-векторы точек N и M ₀ соответственно. Перепишем получен-ное равенство в координатной форме. Имеем

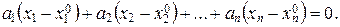
Это уравнение и есть искомое уравнение гиперплоскости Н, которое при n = 3 превращается в уравнение плоскости 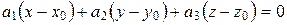, проходящей через точку 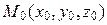перпендикулярно вектору a = (a ₁, a ₂, a ₃).