Покажем, что для любых двух векторов x и y евклидова пространства справедливо неравенство
|(x, y)| 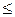
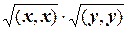 , (9.2)
, (9.2)
называемое неравенством Коши – Буняковского *, причем знак равенства в нем имеет место только в том случае, если векторы x и y линейно зависимы.
В самом деле, если x = 0 или y = 0, то неравенство (9.2) очевидно, поэто-му будем считать, что, например, y 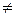 0. Рассмотрим вектор z = x +
0. Рассмотрим вектор z = x + 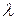 y, где
y, где 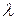 – любое действительное число. Поскольку (z, z)
– любое действительное число. Поскольку (z, z) 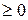 , то имеем
, то имеем
(z, z) = (x + 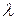 y, x +
y, x + 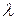 y) = (x, x) + 2
y) = (x, x) + 2 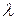 (x, y) +
(x, y) + 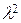 (y, y)
(y, y) 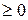 . (9.3)
. (9.3)
При 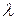 = – (x, y)/(y, y) из неравенства (9.3) получим
= – (x, y)/(y, y) из неравенства (9.3) получим
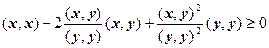 ,
,
или

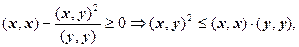
что равносильно неравенству (9.2).
Знак равенства в (9.2) возможен тогда и только тогда, когда (z, z) = 0 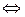
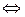 z = x +
z = x + 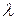 y = 0
y = 0 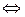 x = –
x = – 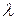 y, т. е. когда векторы x и y линейно зависимы.
y, т. е. когда векторы x и y линейно зависимы.
Из определения скалярного произведения в R n (формула (9.1)) следует, что в R n неравенство Коши – Буняковского принимает вид
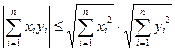 .
.
 2015-08-21
2015-08-21 1633
1633
