Из неравенства Коши – Буняковского для ненулевых векторов получаем
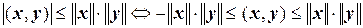 ,
,
или
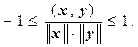
Отсюда следует, что существует, и притом единственное, значение угла j, 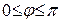 , для которого
, для которого
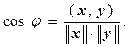 (9.8)
(9.8)
Определение 9.4. Назовем углом между векторами x и y евклидова пространства V угол j, косинус которого определяется соотношением (9.8). Введенное понятие угла между векторами обобщает понятие угла между векторами в R 3.
Если е l, е 2,..., е n – базисные векторы пространства R n, то направляющие косинусы вектора x = (x 1, x 2,…, xn) определим соотношениями
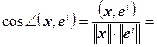
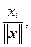 i = 1, 2,…, n,
i = 1, 2,…, n,
где 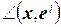 – угол между векторами x и e i из R n.
– угол между векторами x и e i из R n.
Легко проверить, что 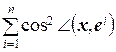 = 1.
= 1.
Умножив ненулевой вектор x на число 1/|| x ||, получим нормированный вектор x 0, длина которого равна единице, т. е.
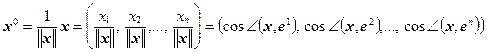 .
.
Отсюда следует, что координатами вектора единичной длины, как и в R 3, служат направляющие косинусы этого вектора.
Определение 9.5. Два вектора x и y из V называются ортогональными, если их скалярное произведение равно нулю, т. е.
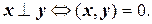
Как и в R 3, считается, что нулевой вектор ортогонален любому вектору x из V.
Из определения косинуса угла между векторами в евклидовом пространстве следует, что для того, чтобы ненулевые векторы x и y были ортогональны, необходимо и достаточно, чтобы cosÐ (x, y) = 0. Введенное понятие ортогональности в евклидовом пространстве соответствует обычному понятию перпендикулярности в R 3.
Отметим, что ортогональность векторов x и y в R n равносильна выполнению равенства
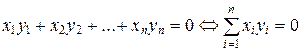 .
.
 2015-08-21
2015-08-21 2046
2046
