Ортогональный базис

Попарно ортогональные векторы в евклидовом пространстве V обладают одним важным свойством.

Покажем, что система попарно ортогональных векторов x ¹, x ²,…, x ^k, не содержащая нулевого вектора, линейно независима. Убедимся, что равенство x ¹ + x ² + … + 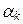x ^k = 0 возможно лишь при = =... = = 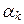0. В самом деле, скалярно умножим обе части этого равенства на x ^j, j = 1, 2,…, k, и, учитывая, что (x ⁱ, x ^j) = 0 при i 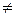j, получим ( 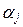x ^j, x ^j) = 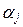(x ^j, x ^j) = 0, j = 1, 2,…, k. Так как (x ^j, x ^j) > 0, то из последнего равенства имеем 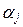= 0, j = 1, 2,…, k.

Определение 9.6. Если число попарно ортогональных ненулевых векторов равно n, где n – размерность пространства, то они образуют базис евклидова пространства, называемый ортогональным базисом. Если же нормы векторов ортогонального базиса равны единице, то базис называется ортонормированным.

Таким образом, базис из векторов u ¹, u ²,..., u ⁿ называется ортонормированным, если

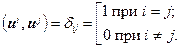
Здесь 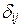– символ Кронекера.

Докажем следующее утверждение.

Теоремa 9.1. Во всяком n-мерном евклидовом пространстве существует ортонормированный базис.

Доказательство. Пусть x ¹, x ²,…, x ⁿ – произвольный базис пространства V. Положим 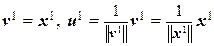. Пусть далее 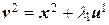, где число 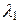подберем так, чтобы векторы v ² и u ¹ были ортогональны, т. е.

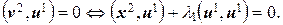
Так как 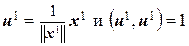, то отсюда находим, что

.

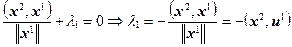При этом значении 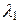вектор 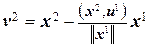ортогонален u ¹. Нормируя v ², получаем, что векторы 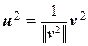и u ¹ образуют ортонормированную пару. Далее, полагая 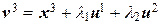и подбирая 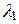и 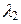так, чтобы выполнялись условия 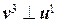и 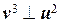, с учетом ортонормированности векторов u ¹ и u ², получаем

;

.

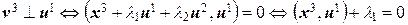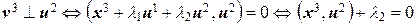Откуда 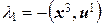, , 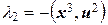т. е. .

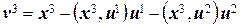Пронормировав v ³, получим вектор 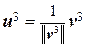, который вместе с u ¹ и u ² образует систему трех ортонормированных векторов. Продолжив этот процесс, после n шагов получим n ортонормированных векторов u ¹, u ²,…, u ⁿ, которые образуют ортонормированный базис.¨

Указанный в теореме 9.1 алгоритм построения ортонормированного базиса называется процессом ортогонализации Грама – Шмидта *, который, учитывая его сложность, рассмотрим более подробно.

Пусть x ¹, x ²,…, x ⁿ – произвольные линейно независимые векторы. Тогда ортонормированная система векторов u ¹, u ²,…, u ⁿ получается по следующей схеме:

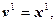
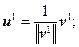
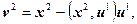
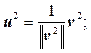
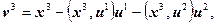
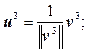
и т. д.

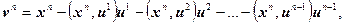
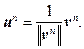
Пример 3. Ортонормировать векторы x ¹ = (1, 0, 0), x ² = (– 2, 1, 2) и x ³ = = (1, – 1, 0) в R ³ со скалярным произведением, заданным формулой (9.1).

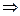
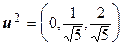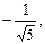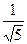
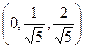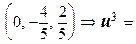
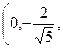
Решение. По методу Грама – Шмидта получаем v ¹ = x ¹ = (1, 0, 0) = u ¹, v ² = = (– 2, 1, 2) – (– 2)(1, 0, 0) = (0, 1, 2) . Далее, т. к. (x ³, u ¹) = 1, (x ³, u ²) = = то v ³ = (1, – 1, 0) – (1, 0, 0) + = 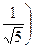. Легко увидеть, что полученные векторы u ¹, u ², u ³ ортонормированны.·

Найдем выражение скалярного произведения в координатах для векторов x и y, заданных в произвольном ортонормированном базисе евклидова пространства V.

Пусть u ¹, u ²,…, u ⁿ – ортонормированный базис пространства V и

x = x ₁ u ¹ + x ₂ u ² +…+ x_n u ⁿ, y = y ₁ u ¹ + y ₂ u ² +…+ y_n u ⁿ –

векторы из V. Тогда в силу аксиом 2° и 3° из §9.1 получим

.

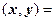
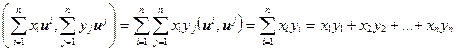Итак, в ортонормированном базисе скалярное произведение двух векторов равно сумме произведений одноименных координат этих векторов.

Выясним смысл координат произвольного вектора x в ортонормированном базисе.

Теоремa 9.2. Координаты вектора в ортонормированном базисе равны ска-лярному произведению этого вектора на соответствующие базисные векторы.

Доказательство. Пусть u ¹, u ²,…, u ⁿ – ортонормированный базис и x = = x ₁ u ¹ + x ₂ u ² +…+ x_n u ⁿ – произвольный вектор. Умножив обе части этого равенства скалярно на вектор u ⁱ, i = 1, 2,..., n, имеем

(x, u ⁱ) = x ₁(u ¹, u ⁱ) +… + x_i (u ⁱ, u ⁱ) +… + x_n (u ⁿ, u ⁱ).

Отсюда получаем

x_i = (x, u ⁱ), i = 1, 2,..., n. ¨

Так как 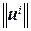= 1, i = 1, 2,..., n, то, как и в R ³, скалярное произведение (x, u ⁱ) = x_i естественно назвать проекцией вектора x на вектор u ⁱ.

Таким образом, координаты вектора x в ортонормированном базисе равны его проекциям на соответствующие базисные векторы.

Итак, формула

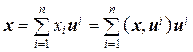
представляет собой разложение произвольного вектора x в ортонормированном базисе u ¹, u ²,…, u ⁿ евклидова пространства.