Знакоопределенные квадратичные формы

Определение 15.3. Квадратичная форма Q (x) = Q (x ₁, x ₂,…, x_n) называется положительно (отрицательно) определенной, если Q (x) > 0 (Q (x) < 0), " x Î R ⁿ, x ¹ 0. Квадратичная форма Q (x) называется неотрицательно (неположительно) определенной, если Q (x) ³ 0 (Q (x) £ 0), " x Î R ⁿ. Матрица А, соответствующая положительно (отрицательно) определенной форме Q (x) = (x, А x), называется положительно (отрицательно) определенной матрицей. Положительно и отрицательно определенные квадратичные формы называются знакоопределенными.

Например, квадратичная форма Q (x ₁, x ₂, x ₃) = 3 x ₁² + 5 x ₂² + 4 x ₃² является, очевидно, положительно определенной. А форма Q (x ₁, x ₂, x ₃) = (4 x ₁ – 5 x ₂ – x ₃)² = = 16 x ₁² – 40 x ₁ x ₂ – 8 x ₁ x ₃ + 25 x ₂² + 10 x ₂ x ₃ + x ₃² является неотрицательно определенной, т. к. она обращается в нуль, например, при x = (x ₁, 0, 4 x ₁) ¹ 0, если x ₁ ¹ 0.

Теоремa 15.2. Для того чтобы квадратичная форма Q (x) = (x, А x) была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения l ₁, l ₂,…, l_n матрицы А квадратичной формы были положительными (отрицательными). Для того чтобы квадратичная форма была неотрицательно (неположительно) определенной, необходимо и достаточно, чтобы все собственные значения l ₁, l ₂,…, l_n матрицы квадратичной формы были неотрицательными (неположительными), среди которых найдутся нулевые.

Доказательство. Необходимость. Пусть Q (x) = (x, А x) > 0, " x ¹ 0. Если l_i – собственное значение матрицы А, соответствующее собственному вектору x ⁱ, i = 1, 2,..., n, то Q (x ⁱ) = (x ⁱ, A x ⁱ) = (x ⁱ, l_i x ⁱ) = l_i (x ⁱ, x ⁱ) > 0. Отсюда, т. к. (x ⁱ, x ⁱ) > 0, получаем, что l_i > 0, i = 1, 2,..., n.

Достаточность. Пусть l_i > 0, i = 1, 2,..., n. Тогда из формулы (15.4) следует, что Q (x) > 0, " x ¹ 0.

Аналогично проводится доказательство для отрицательно (неотрицательно, неположительно) определенной квадратичной формы.¨

Следствие. Матрица знакоопределенной квадратичной формы является невырожденной. Определитель матрицы положительно определенной квадратичной формы положителен. Определитель матрицы неотрицательно (неположительно) определенной квадратичной формы равен нулю.

Доказательство. Пусть Т – матрица ортогонального преобразования, приводящая квадратичную форму с матрицей А к каноническому виду с матрицей L = diag (l ₁, l ₂,…, l_n). Тогда имеем

L = Т ^{– 1} АТ Û А = ТLТ ^{– 1} Þ | A | = | T | × | L |×| Т ^{– 1}| = | L | = l ₁ l ₂… l_n.

Отсюда и из теоремы 15.2 вытекает справедливость данного следствия.¨

Из теоремы 15.2 следует, что преобразование z_i = 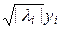при l_i ¹ 0, z_i = y_i при l_i = 0, i = 1, 2,..., n, приводит канонический вид (15.3) квадратичной формы к виду

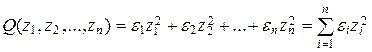, (15.5)

где e_i = ± 1 при l_i ¹ 0, e_i = 0 при l_i = 0, i = 1, 2,..., n.

Определение 15.4. Канонический вид (15.5) называется нормальным видом квадратичной формы.

Определение 15.5. Пусть A = [ a_ij ], i, j = 1, 2,..., n, – квадратная матрица. Угловыми минорами порядков 1, 2,…, n матрицы А называются все миноры соответствующих порядков, расположенные в левом верхнем углу матрицы А:

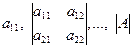. (15.6)

Теоремa 15.3 (критерий Сильвестра* положительной определенности квадратичной формы). Для того чтобы квадратичная форма Q (x) = (x, А x) была положительно определенной, необходимо и достаточно, чтобы все угловые миноры матрицы A были положительны:

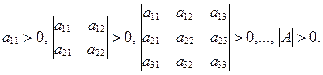(15.7)

Доказательство. Необходимость. Пусть квадратичная форма положительно определена. Тогда | А | > 0 в силу следствия из теоремы 15.2. Для вектора x = (x ₁, 0,..., 0) ¹ 0 имеем Q (x) = a ₁₁ x ₁² > 0 Þ a ₁₁ > 0. Если x = (x ₁, x ₂, 0,..., 0) ¹ 0, то на основании того же следствия имеем

Q (x) = .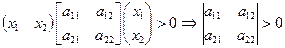

Продолжая этот процесс последовательно, получим все соотношения (15.7).

Достаточность. Доказывается методом математической индукции по числу переменных квадратичной формы с помощью теорем 15.1, 15.2 и формулы (15.5).¨

Замечание 1. Если квадратичная форма является неотрицательно определенной, то все угловые миноры (15.6) ее матрицы неотрицательны. Доказательство проводится аналогично доказательству теоремы 15.3 с учетом теорем 15.1 и 15.2.

Замечание 2. Очевидно, квадратичная форма Q (x) является отрицательно (неположительно) определенной тогда и только тогда, когда квадратичная форма – Q (x) является положительно (неотрицательно) определенной. Матрицы этих двух форм отличаются друг от друга только множителем – 1. Следовательно, согласно свойству 3 определителей, их угловые миноры одинакового четного порядка равны, а угловые миноры одинакового нечетного порядка различаются лишь знаком.

Следствие (критерий отрицательной определенности квадратичной формы). Для того чтобы квадратичная форма Q (x) = (x, А x) была отрицательно определенной, необходимо и достаточно, чтобы все угловые миноры нечетных порядков матрицы A были отрицательны, а все угловые миноры четных порядков матрицы A были положительны:

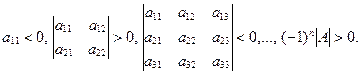
Замечание 3. Если квадратичная форма является неположительно определенной, то все угловые миноры нечетных порядков ее матрицы неположительны, а все угловые миноры четных порядков ее матрицы неотрицательны. Данное утверждение вытекает из замечаний 1 и 2.

Пример 4. Исследовать на знакоопределенность квадратичную форму

Q (x ₁, x ₂, x ₃) = x ₁² + 2 x ₁ x ₂ + 2 x ₁ x ₃ + 2 x ₂² + 4 x ₂ x ₃ + 3 x ₃².

Решение. Матрица этой формы имеет вид .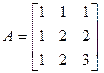

Вычислим значения всех угловых миноров матрицы A:

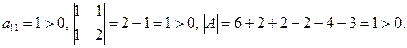
В соответствии с критерием Сильвестра данная квадратичная форма является положительно определенной.·

* Дж. Дж. Сильвестр (1814 – 1897) – английский математик.