Пусть A – самосопряженный оператор. По теореме 12.4 у него существует n попарно ортогональных собственных векторов. Если эти векторы нормировать и взять в качестве базиса пространства, то в силу теоремы 14.1 матрица оператора A в этом базисе будет диагональной. Таким образом, для всякого самосопряженного оператора существует такой ортонормированный базис, что матрица этого оператора имеет в нем диагональный вид. Матрица перехода Т к этому базису, очевидно, ортогональная, т. е. Т – 1 = Т *. Таким образом, с учетом формулы (14.1), установлено следующее утверждение.
Теоремa 14.2. Если А – симметрическая матрица, то существует ортогональная матрица Т, такая, что Т * АТ – диагональная матрица.
Из вышеизложенного в §14.1 получаем следующий алгоритм приведения матрицы А к диагональному виду:
1) находим собственные значения и соответствующие им собственные векторы матрицы А, образующие базис пространства R n, и переходим к шагу 2; если не существует базиса пространства R n, состоящего из собственных векторов матрицы А, то матрица А не диагонализируема;
2) составляем матрицу перехода Т, столбцами которой служат координаты собственных векторов матрицы А, образующие базис пространства R n;
3) находим Т – 1 и по формуле (14.1) получаем искомую диагональную матрицу L.
Если А – симметрическая матрица, то ее собственные векторы необходимо нормировать при составлении матрицы T, и тогда
L = Т * АТ. (14.2)
Пример 2. Привести к диагональному виду матрицу
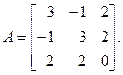
Решение. Характеристическое уравнение
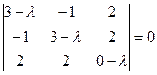
имеет корни l 1 = –2, l 2 = l 3 = 4. Для l 1 = –2 и l 2 = 4 находим соответствующие собственные векторы x 1 = (1, 1, – 2) и x 2 = (2, 0, 1) (см. аналогичный пример 1 из §12.2). Поскольку x 3 ^ x 1 и x 3 ^ x 2 в силу теоремы 12.4, то в качестве третьего собственного вектора можно взять вектор x 3 = [ x 1, x 2] = (1, – 5, – 2) – векторное произведение x 1 и x 2. Пронормировав векторы x 1, x 2 и x 3, получим
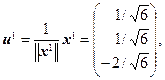
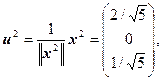
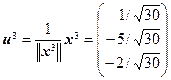 .
.
Координаты этих векторов образуют столбцы матрицы Т. Тогда согласно (14.2)
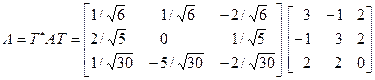
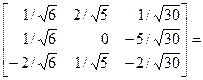
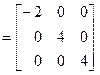 .·
.·
 2015-08-21
2015-08-21 5208
5208
