2015-08-21
22768
Как следует из теоремы 13.1, матрица линейного оператора зависит от базиса пространства. Как подобрать этот базис, чтобы матрица линейного оператора в нем имела наиболее простой вид? На этот вопрос отвечает следующая теорема.
Теоремa 14.1. Для того чтобы матрица линейного оператора A: R n ® R n в некотором базисе была диагональной, необходимо и достаточно, чтобы этот базис состоял из собственных векторов линейного оператора A.
Доказательство. Необходимость. Пусть матрица линейного оператора A в некотором базисе е l, е 2,..., е n диагональная, т. е.
.
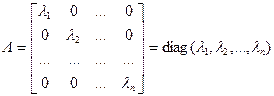Тогда, очевидно, справедливы равенства Aе j = L е j = lj е j, j = 1, 2,..., n, из которых следует, что lj – собственные значения, а е j – соответствующие им собственные векторы оператора A.
Достаточность. Предположим, что базис пространства состоит из собственных векторов x 1, x 2,…, x n, а l 1, l 2,…, ln – соответствующие им собственные значения оператора A. Тогда Ax j = lj x j, j = 1, 2,..., n. Отсюда следует, что L = = diag (l 1, l 2,…, ln) – матрица линейного оператора A в базисе x 1, x 2,…, x n. ¨
|
|
|
Определение 14.1. Если существует базис пространства R n, состоящий из собственных векторов x 1, x 2,…, x n линейного оператора A: R n ® R n с матрицей А в некотором базисе пространства R n, и Т – матрица перехода от этого базиса к базису x 1, x 2,…, x n, то справедливо равенство
L = Т –1 АТ, (14.1)
где L – диагональная матрица с собственными значениями, соответствующими собственным векторам оператора A, на главной диагонали. В этом случае матрица А линейного оператора A называется диагонализируемой.
Пример 1. Привести к диагональному виду матрицу
.
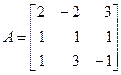Решение. Для этой матрицы в примере 1 из §12.2 найдены собственные векторы x 1 = (–1, 1, 1), x 2 = (11, 1, –14)и x 3 = (1, 1, 1), соответствующие собственным значениям l 1 = 1, l 2 = – 2 и l 3 = 3. Поскольку все собственные значения попарно различны, векторы x 1, x 2, x 3 образуют базис пространства R 3 согласно теореме 12.1. Значит, согласно определению 14.1 матрица А диагонализируема.
Составим матрицу перехода Т к базису x 1, x 2, x 3, столбцами которой будут координаты данных базисных векторов.
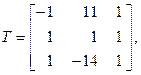
откуда
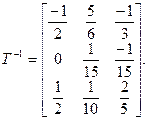
Тогда
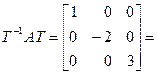diag (1, – 2, 3).·
