Выясним, как преобразуется матрица линейного оператора при переходе от одного базиса к другому.
Теоремa 13.1. Пусть u 1, u 2,…, u n и v 1, v 2,…, v n – два базиса в R n, а Т – матрица перехода от старого базиса к новому. Если А – матрица линейного оператора A в базисе u 1, u 2,…, u n, то матрицей В этого оператора в новом базисе v 1, v 2,…, v n является матрица
В = Т – 1 AT. (13.7)
Доказательство. Пусть y = А x, " x Î R n, где векторы x и y рассматриваются в базисе u 1, u 2,…, u n. Если v 1, v 2,…, v n – новый базис и Т – матрица перехода, то в силу равенства (13.5) x = Т x ¢ и y = Т y ', где x ¢ и y ' – векторы x и y в новом базисе v 1, v 2, …, v n. Подставив x и y в равенство y = А x, получим равенство
Т y ' = АТ x ' Û y ' = Т – 1(АТ x ') Û y ' = (Т – 1 АТ) x ¢,
справедливое в новом базисе v 1, v 2,…, v n. Отсюда и следует, что матрица линейного оператора в новом базисе v 1, v 2,…, v n находится по формуле (13.7).¨
Следствие. Определитель матрицы линейного оператора не зависит от базиса пространства.
Доказательство. В самом деле, согласно свойствам определителей, имеем
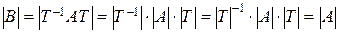 .¨
.¨
Определение 13.3. Матрицы А и В = Т – 1 АТ называются подобными.
Из теоремы 13.1 следует, что подобные матрицы являются матрицами одного и того же линейного оператора A: R n ® R n, но рассматриваемого в разных базисах с матрицей перехода Т.
Пример 2. В базисе u 1, u 2 оператор A имеет матрицу
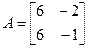 .
.
Найти матрицу этого оператора в базисе v 1= u 1 +2 u 2, v 2 = 2 u 1 +3 u 2.
Решение. Определяем матрицу перехода и обратную ей матрицу:
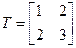 , Т – 1 =
, Т – 1 = 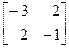 .
.
Тогда искомая матрица, согласно формуле (13.7), имеет вид
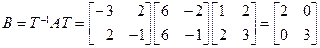 .·
.·
Справедлива следующая теорема.
Теоремa 13.2. Собственные значения подобных матриц совпадают.
Доказательство. В самом деле, характеристический многочлен матрицы В равен характеристическому многочлену матрицы А:
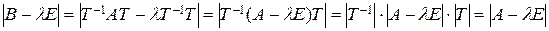 .¨
.¨
 2015-08-21
2015-08-21 9560
9560








