Определение 15.1. Квадратичной формой от n переменных x 1, x 2,…, xn называется многочлен
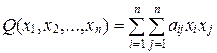 , (15.1)
, (15.1)
где все aij = aji – действительные числа, называемые коэффициентами квадратичной формы.
Для записи квадратичной формы в матричном виде из переменных x 1, x 2,…, xn образуем вектор-столбец x, а из коэффициентов aij – матрицу
А 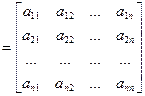 ,
,
которая называется матрицей квадратичной формы и является в силу равенств aij = aji, i, j = 1, 2,..., n, симметрической.
Учитывая правило умножения матрицы на вектор, получаем
А x 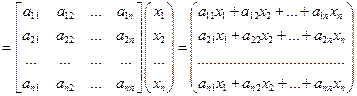 .
.
Тогда выражение (15.1) запишется в виде
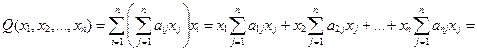 (x, А x),
(x, А x),
или в виде
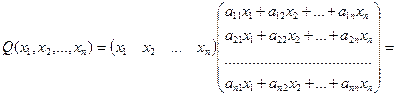 x * А x,
x * А x,
где x * – вектор-строка из переменных x 1, x 2,…, xn, знак «*» означает транспонирование.
Итак, в матричной записи квадратичная форма (15.1) имеет вид
Q (x 1, x 2,…, xn) = (x, А x) = x * А x. (15.2)
Таким образом, квадратичная форма полностью определяется своей матрицей, и, наоборот, любая квадратичная форма определяет однозначно симметрическую матрицу.
Пример 1. Составить матрицу квадратичной формы
Q (x 1, x 2, x 3) = 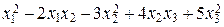 .
.
Решение. Учитывая, что в квадратичной форме коэффициенты aij = aji, получаем а 11 = 1, а 12 = а 21= – 1, а 13 = а 31= 0, а 22 = – 3, а 23 = а 32= 2, а 33 = 5. То есть искомая матрица имеет вид
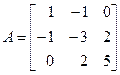 .
.
Можно проверить по формуле (15.2), что
(x, А x) = (x 1, x 2, x 3) × (x 1 – x 2, – x 1 – 3 x 2 + 2 x 3, 2 x 2 + 5 x 3) = Q (x 1, x 2, x 3),
x * А x = 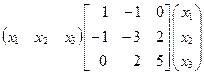 = Q (x 1, x 2, x 3).·
= Q (x 1, x 2, x 3).·
Пример 2. Найти квадратичную форму, соответствующую матрице
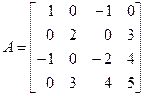 .
.
Решение. Данной матрице соответствует квадратичная форма
Q (x 1, x 2, x 3, x 4) = 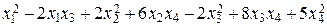 .·
.·
 2015-08-21
2015-08-21 6459
6459
