Бифуркации динамических систем

Если внимательно присмотреться к окружающей нас природе, то можно сделать следующее интересное наблюдение. Жизнь на планете Земля возможна лишь благодаря тепловому излучению Солнца, которое служит источником энергии. Летом северное полушарие получает световой энергии больше, чем зимой. И картина летней природы при этом заметно отличается от зимней. Можем рассмотреть в качестве примера объем воды в озере. Количественной мерой привносимой солнечной энергии является температура воды. Летом вода в озере теплая и можно купаться. С наступлением осени температура воды постепенно уменьшается. Купаться уже не хочется, однако вода и при более низкой, но плюсовой температуре остается водой! Глубокой осенью верхний слой воды в озере остывает до нулевой температуры и вдруг превращается в лед! Далее и при −20°C лед остается льдом. При прохождении температуры через нуль вода резко изменила свои свойства: она из жидкого состояния перешла в твердое. И не плавно, а скачком. Если рассматривать температуру воды как некий параметр системы, то хорошо известно, что с изменением параметра вода резко меняет свои свойства при переходе через 0°С, через 100°C, когда вода превращается в пар. Есть и другие особые значения температуры воды. Оказывается, что большинство интересных физических задач при их математическом описании при- водят к дифференциальным уравнениям, зависящим от одного или нескольких параметров.

В качестве другого примера рассмотрим уравнения колебаний обыкновенного маятника или (что с математической точки зрения полностью идентично) параллельного RLC-контура:

x˙˙+αx˙ ω0^2x = 0

Уравнение содержит два параметра: α – параметр затухания, характеризующий трение, и ω0 – параметр, определяющий частоту колебаний. Если потери энергии отсутствуют (параметр затухания α = 0), то решением уравнения будут гармонические незатухающие колебания. При малом трении 0 < α < 1 движение системы будет колебательным с амплитудой, которая уменьшается во времени по экспоненциальному закону. Наконец, при достаточно большом трении (α > 1) движение маятника будет апериодическим, затухающим во времени. Уже в этом простом примере выделяются два особых значения параметра α = 0 и α = 1, отклонения от которых качественно меняют свойства системы.

Изменение параметра в уравнении может вызвать потерю устойчивости одного состояния (или режима функционирования) системы и переход ее в другое, отличное от первого состояние. Это явление, как сказано выше, называется бифуркацией (от слова раздвоение), а значение параметра, при котором оно происходит, – точкой бифуркации. Состояние системы ниже точки бифуркации и выше ее при изменении параметра все- таки меняется. Ясно, что вода при температуре +3 и +22°C – это разные состояния. Но при этом вода остается водой! В математике и физике существует понятие грубости или структурной устойчивости. Суть этого понятия в том, что при малом изменении параметра грубая система хоть и изменяет в деталях режим функционирования, но не принципиально. С этой точки зрения для грубых систем переход через точку бифуркации означает смену одного структурно устойчивого режима на другой. При этом в точке бифуркации система не является грубой: малое изменение параметра в ту или иную сторону приводит к резким изменениям состояния.

Мы условились, что в уравнении (8) параметры a и b положительны. Устойчивость определяется знаком производной правой части уравнения (8) в стационарной точке, то есть знаком величины λ (10). При положительных значениях параметров a и b эта производная всегда отлична от нуля. А что, если мы будем уменьшать значение параметра a? Как видно из (10), при a = 0 (независимо от величины b > 0) величина λ обращается в нуль, возмущение y не нарастает и не затухает. Мало того, при a = 0 в системе (2) оба стационарных состояния как бы сливаются в одно (x = 0)! Далее, если a < 0, то стационарных состояний нет вовсе.

Приведем теперь результаты математического анализа этой бифуркации, которая известна как бифуркация “двукратное равновесие”. Вновь рассмотрим уравнение (8). Пусть x0 (a) есть грубое состояние равновесия, то есть λ(a) ­ 0. Это означает, что при малой вариации параметра a состояние x0 (a) продолжает существовать как устойчивое или неустойчивое стационарное состояние.

При некотором значении параметра a = a* собст- венное число λ(a*) в стационарном состоянии может обратиться в нуль:

λ(а) = dF/dx |x0 = 0, a=a*. (13)

Для реализации бифуркации “двукратное равновесие” необходимо, чтобы вторая производная была отлична от нуля:

d2F/ ∂x^2 |x0 ≠ 0

Значение параметра a*, при котором выполняется условие (13), является точкой бифуркации. До точки бифуркации a < a* мы имеем два стационарных состо- яния. В точке бифуркации a = a* они сливаются в одно, далее при a > a* этих состояний в системе не будет. В нашем случае (8) a* = 0.

Результаты можно представить графически

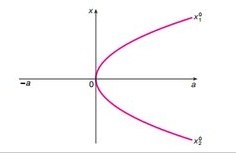
Бифуркация “двукратное равновесие”.

При a > 0 в системе (8) два стационарных состояния и при a = 0 они сливаются в одно, и при a <0 стационарные состояния исчезают x1 0 x

“Мягкие” и “жесткие” бифуркации.

Несмотря на многолетнюю историю существования и развития классической теории устойчивости и бифуркаций, наступил момент, когда к этой теории было вдруг привлечено всеобщее внимание. Причиной тому послужили популярно изложенные версии работ французского математика Рене Тома по так называемой теории катастроф. Теория катастроф в начале 70-х годов стала модной, понятной для неспециалистов и универсальностью своих претензий стала напоминать псевдонаучные теории прошлых времен. Появление теории катастроф Р. Тома специалистами не было воспринято как новое открытие, хотя некоторые результаты этой теории заслуживают самого глубокого уважения. Но принципиального научного открытия здесь нет.

Речь шла все о тех же бифуркациях, но при этом выбирался один из типов – так называемые жесткие бифуркации. Для пояснения рассмотрим два простых примера. В первом случае (рис. 2) в результате бифуркации исходное стационарное состояние теряет устойчивость и рождаются два новых устойчивых стационарных состояния. При этом вновь появившиеся два стационарных состояния расположены в непосредственной близости от исходного состояния,

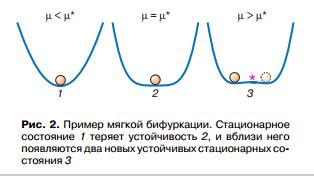
которое потеряло устойчивость. Бифуркации такого типа называют мягкими, имея в виду, что вновь родившийся режим функционирования системы как бы появляется из режима, потерявшего устойчивость, и сосуществует рядом с ним.

Другой пример бифуркации качественно представ- лен на рис. 3. При µ < µ* (рис. 3, 1) шарик находится в устойчивом стационарном состоянии. При этом существует еще одно, неустойчивое состояние. В точке бифуркации µ = µ* устойчивое и неустойчивое состояния сливаются в одно. Далее они исчезают, и система выбирает новый режим на который существенно отличается от предыдущего и не находится в непосредственной близости от исходного режима.

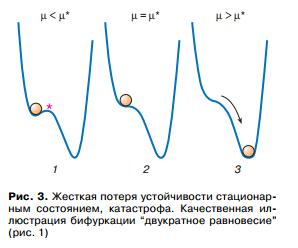Такой тип бифуркаций называют жестким, и именно жесткие бифуркации явились предметом анализа в теории катастроф.