2015-08-21
276
Скористаємося в рівнянні (1.1) розкладанням в ряд Тейлора
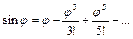(1.2)
Для достатньо малих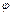 
можемо знехтувати в (1.2) усіма членами, за винятком 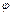. Після спрощення виразу отримаємо основне диференціальне рівняння задачі про вільні коливання:
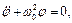(1.3)
де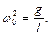 
Загальний розв’язок цього рівняння має вигляд
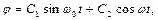
який і висловлює принцип суперпозиції коливань в лінійних системах.
Можна користуватися і іншою формою запису розв’язок:
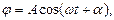(1.4)
яке представляє собою незгасаючі гармонійні коливання. Тут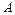 
– амплітуда коливань, 
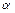– початкова фаза, які знаходяться за початковими умовами. Кругова частота 
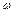пов'язана з фізичними параметрами системи і не залежить від початкових умов. З цієї причини її називають власною частотою системи.
