Вільні коливання систем з двома ступенями свободи

Розглянемо вільні коливання механічної системи, що має два ступені свободи. Прикладами таких систем є: механічна система пов'язаних маятників (рис. 4.1), пов'язані електричні контури (рис. 4.2), трьохатомна молекула (рис. 4.3).

Рисунок 4.1– Пов'язані маятники

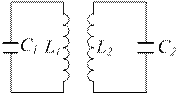
Рисунок 4.2 – Коливальні контури з індуктивним зв'язком

Рисунок 4.3 – Трьохатомна молекуда води

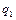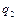Використовуючи вирази кінетичної і потенційної енергій системи в узагальнених координатах і , рівняння Лагранжа призводять до диференціальних рівнянь вільних коливань виду

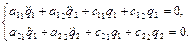(4.1)

Уявімо систему (4.1) у формі

(4.2)

звідки видно, що ліві частини є рівняннями лінійних консервативних систем, а праві частини характеризують сили зв'язку між ними. Коефіцієнти 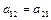, 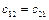характеризують зв'язок між так званими парціальними системами.

Будь-яку складну систему з двома ступенями свободи можна розглядати як систему, що складається з двох окремих систем з одним ступенем свободи, пов'язаних одна з однією. Ці окремі системи називають парціальними. Зв'язність систем означає, що коливання в одній системі впливають на коливання в інший і навпаки.

Приймемо для подальшого вивчення коливання системи, що парціальна система, відповідна даної незалежної координаті, отримана з повної, коли всі координати системи, крім данної, рівні тотожно нулю.

З (4.2) видно, що парціальні частоти рівні

, .

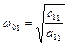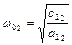З властивостей позитивної визначеності квадратичних форм Т та П випливає, що

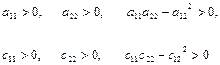(4.3)

(критерій Сильвестра).

Частинні розв’язки системи (4.1) шукаємо у вигляді простого гармонійного закону:

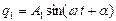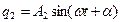, . (4.4)

Підставляючи (4.4) в рівняння (4.1), одержимо рівняння для амплітуд

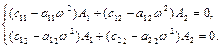(4.5)

Позначимо відношення узагальнених координат, рівне відношенню амплітуд коливань, через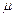

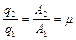. (4.6)

Нетривіальний розв’язок системи (4.5) буде тільки в тому випадку, коли її визначник дорівнює нулю, що дає рівняння власних частот коливань

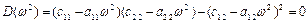. (4.7)

або

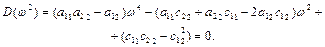(4.8)

Досліджуємо функцію 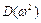. Коефіцієнт при 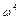(див. 4.8) і вільний член більше нуля згідно критерію Сильвестра (4.3): це означає, що графік функції є парабола з вітками, спрямованими вгору. З (4.8) видно, що при 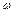рівної однієї з парціальних частот 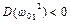та 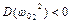. Корені рівняння (4.8) визначають власні частоти системи.

Зобразимо графік функції 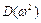(рис. 4.4).

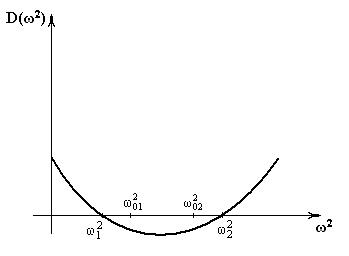
Рисунок 4.4 – Закон розподілу власних частот системи

Графік ілюструє відому теорему Релея: нижча частота 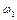власних коливань системи завжди менше найменшої парціальної частоти 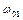, а вища частота завжди більше найбільшої парціальної частоти .

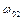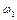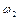Відповідні частотам і коливання називають головними коливаннями системи. Меншу з частот 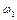називають основною частотою, а перше головне коливання називають основним коливанням (воно є основним у результуючому русі системи). Визначивши 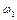і 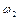, з рівняння (4.8) знайдемо два значення 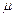, відповідні кожному з головних коливань:

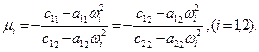(4.9)

Величини 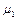, 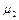характеризують форми головних коливань і їх називають коефіцієнтами розподілу амплітуд, тобто вони показують у скільки разів амплітуда відповідного коливання в одній з координат більше (або менше) амплітуди іншої координати.

Позначивши значення узагальнених координат і амплітуд коливань, відповідних першому головному коливанню, індексом (1), маємо

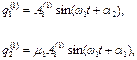(4.10)

для другого головного коливання - індексом (2), то

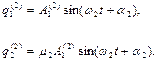(4.11)

Загальний розв’язок системи диференціальних рівнянь (4.1) виходить шляхом підсумовування частинних розв’язків

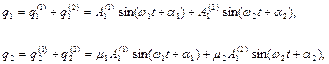(4.12)

де 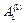, , 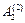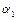і 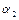знаходяться з початкових умов.

Висновки:

1. Розв’язок (4.12) показує, що кожне з головних коливань окремо є простим гармонійним коливанням, але результуючий рух являє собою складний рух.

2. Якщо система здійснює одне з головних коливань (див. 4.12), то обидві узагальнені координати змінюються синхронно, тобто мають однакові частоти і фази коливань.

3. У кожному з головних коливань амплітуди знаходяться в постійному співвідношенні (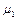 або 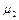), що не залежить від початкових умов і залежить тільки від структури системи.

Биття

Розглянемо систему з двома ступенями свободи за умови близькості власних частот: 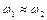. Тоді розв’язок (4.12) для узагальненої координати, наприклад,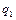

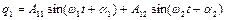(4.13)

можна записати у вигляді

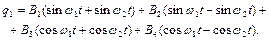(4.14)

Введемо позначення:

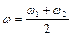и ,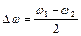

які називають «середньою» частотою і частотою «модуляції» відповідно. Замість (4.14) зручно записати

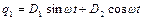, (4.15)

де 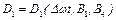, 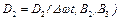– повільно мінливі періодичні функції часу.

Остаточно отримуємо замість (4.13) функцію

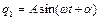, (4.16)

де , ,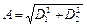

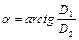тобто рух носить синусоїдальний характер з амплітудою, що періодично повільно змінюється. Графік зміни 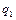зображений на рис. 4.5.

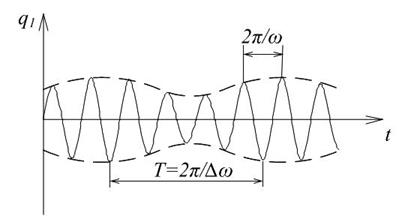
Рисунок 4.5 – Графік биття однієї узагальненої координати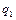

Такі коливання називаються биттям. Рух, відповідний координаті 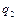, також відбувається за законом биття, але зрушеним по фазі щодо 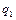. Цей факт свідчить про обмін енергією між ступенями свободи.

Відзначимо, що в будь-якій системі з двома ступенями свободи можна створити биття.