Модели скользящего среднего

Модель скользящего среднего предполагает, что в ошибках модели в предшествующие периоды сосредоточена информация обо всей предыстории ряда. В этой модели каждое новое значение - среднее между текущей флуктуацией и несколькими (в частности, одной) предыдущими ошибками.

Модели скользящего среднего порядка q, обозначаемые CC(q), в англоязычной литературе MA(q) (Moving Average models), имеют вид:

у_t = e_t - q₁ e_t-1 - q₂ e_t-2 -…- q_q e_t-q, (3.14)

где e_t — “ белый шум”.

Широко распространены в статистической практике модели скользящего среднего 1-го (q = 1) и второго порядка (q = 2):

МА(1): у_t = e_t - q e_t-1; (3.15)

МА(2): у_t = e_t - q₁ e_t-1 - q₂ e_t-2. (3.16)

Рассмотрим модель скользящего среднего 1-го порядка — МА (1). Преобразуем (3.15), последовательно выражая e_t-1, e_t-2, e_t-3 и т.д.:

e_t = у_t + q e_t-1 = у_t + q (y_t-1 - q e_t-2) = у_t + q y_t-1

₊q ²(у_t-2 + q e_t-3) = y_t+q y_t-1 + q ² у_t-2 +q ³(у_t-3 + q e_t-4) =

= y_t+q y_t-1 + q ² у_t-2 +q ³ у_t-3 + …

Это выражение можно переписать в виде:

у_t = e_t - 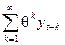. (3.17)

Таким образом, ряд у_t,сгенерированный моделью МА (1), может быть представлен также в виде модели авторегрессии бесконечного порядка. В моделях скользящего среднего МА (q) не требуется накладывать никаких ограничений на параметры q₁, q₂,..., q_q для обеспечения стационарности ряда. Однако, если в модели МА(1) параметр q по абсолютной величине больше или равен 1, то текущее значение у_t в соответствии с (3.17) будет зависеть от своих прошлых значений у_t-1 , у_t-2,..., берущихся с весами, бесконечно растущими по мере удаления в прошлое. Чтобы избежать этого, надо, чтобы веса в (6.21) образовывали сходящийся ряд, т.е. чтобы | q | < 1.

Отметим, что подобно тому, как ряд, генерированный моделью скользящего среднего первого порядка МА (1), может быть представлен в виде модели авторегрессии бесконечного порядка AR (¥), также существует представление A R (1) в виде МА (¥). При этом на параметры процесса AR (p) не накладываются никакие условия для того, чтобы этот процесс был обратимым. Но для стационарности процесса корни его характеристического уравнения должны лежать вне единичного круга. В то же время параметры процесса МА(q) не должны удовлетворять никаким условиям для стационарности, однако для обратимости корни его характеристического уравнения

1 - q₁z - q₂ z² -... - q_q z^q = 0.= 0

должны лежать вне единичного круга.

Найдем выражение для АКФ процесса МА(q). Для этого представим y_t-k в виде соотношения (3.14):

y_t-k = e_t-k - q₁e_t-k-1- q₂e_t-k-2 -…- q_qe_t-k-q. (3.18)

Перемножим соответственно левые и правые части уравнений (6.18) и (6.22), а затем возьмем математическое ожидание от получившегося выражения. При этом следует учесть, что элементы белого шума e_t1 и e_t2 не коррелируют при t₁ ¹ t₂.

Тогда выражение для ковариации М(y_t у_t-t) = g(t) примет вид:

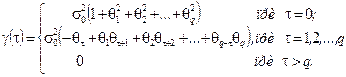(3.19)

АКФ получается путем деления (3.19) на дисперсию процесса g(0):

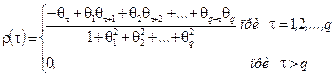(3.20)

Таким образом, АКФ процесса МА(q) равна нулю для всех значений t, больших порядка q. Это важное характеристическое свойство модели.

На практике наиболее часто используют частный случай модели — модель скользящего среднего 1-го порядка МА(1):

у_t = e_t - q e_t-1

где e_t — “белый шум”.

Как уже было показано ранее, для обратимости процесса необходимо выполнение условия | q | < 1.

Очевидно, что М (у_t) = 0; D (y_t) = .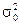

АКФ согласно (3.20) определяется выражением

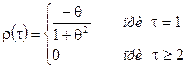. (3.21)

ЧАКФ r_ч (t) задается выражением

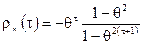(3.22)

Поведение ЧАКФ определяется затухающей экспонентой. Если значение r (1) положительно, то параметр 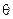< 0, следовательно, r_ч (t) осциллирует с переменным знаком. Если значение r(1) отрицательно, то параметр 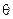> 0, следовательно, все значения r_ч (t) отрицательны.

Отмеченные свойства моделей скользящих средних позволяют сформулировать следующие практические рекомендации по их идентификации.

Для моделей МА(1):

• автокорреляционная функция имеет выброс (пик) при лаге, равном 1, а остальные значения статистически незначимы;

• частная автокорреляционная функция экспоненциально затухает (либо монотонно, либо осциллируя, т.е. меняя знак).

Для моделей МА(2):

• автокорреляционная функция имеет выбросы (пики) на лагах, равных 1 и 2, а остальные значения статистически незначимы;

• частная автокорреляционная функция имеет форму синусоиды или экспоненциально затухает.

3.4 Модели авторегрессии cо скользящими
средними в остатках

На практике для наглядности описания анализируемого экономического процесса в модель могут быть включены как члены, описывающие авторегрессионные составляющие, так и члены, моделирующие остаток в виде процесса скользящих средних. Такой процесс называется - АРСС (р, q) или, как принято в англоязычной литературе, AutoRegressive-Moving Average (ARMA (р, q)). Параметры р и q определяют соответственно порядок авторегрессионной составляющей и порядок скользящих средних.

Модель ARMA(p, q) имеет вид:

y_t=a₁ y_t-1 + a₂ y_t-2 +_… + a_py_{t-p +} e_p- q₁e_t-1- q₂e_t-2 -…- q_qe_t-q. (3.23)

Такая модель может интерпретироваться как линейная множественная регрессия. В качестве объясняющих переменных в ней выступают предыдущие значения самой зависимой переменной, а в качестве регрессионного остатка - скользящие средние из элементов белого шума.

Чтобы процесс (3.23) был стационарным, необходимо и достаточно, чтобы все корни характеристического уравнения AR(p) -npoцесса лежали вне единичного круга:

1 - a₁z - a₂ z² -... - a_p z ^p = 0. (3.24)

Аналогично, для обратимости процесса (3.23) необходимо и достаточно, чтобы все корни характеристического уравнения процесса МА(q) лежали вне единичного круга:

1 - a₁z - a₂ z² -... - a_q z ^q = 0 (3.25)

Простейший смешанный процесс ARMA(1,1):

y_t=a₁ y_{t-1 +} e_p - q₁e_t-1 (3.26)

Это уравнение можно преобразовать к виду:

y_t+a₁ y_t-1 = e_p - q₁e_t-1 (3.27)

Стационарность процесса ARMA(1,1) обеспечивается условием | a | < 1, а обратимость, в свою очередь, гарантируется выполнением условия | q | <1.

Автоковариационные функции процесса ARMA(1,1):

g (0) = 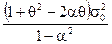, (3.28)

g (1) = 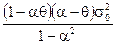. (3.29)

Значение автоковариационной функции для лага t больше 1 определяется следующим рекуррентным соотношением:

g (t) = a g (t -1) при t > 1. (3.30

Следовательно, значения АКФ будут иметь вид

r (1) = 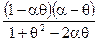(3.31)

r (t) = a r (t -1) = a ^{t -1} r (1) при t > 1. (3.32)

Из (3.31),(3.32) видно, что, хотя выражение для r (1) отличается от соответствующего выражения для процесса AR (1), соотношение между r (1) и последующими значениями АКФ такое же. Таким образом, для процесса ARMA (1,1) значения АКФ будут экспоненциально убывать от значения r (1), причем если a положительно, — то монотонно, если отрицательно, — то знакопеременно.

Поведение ЧАКФ определяется начальным значением r_ч (1), после которого функция экспоненциально убывает. Если q положительно, то функция убывает монотонно, если отрицательно, — то знакопеременно.

Исследования показывают, что при использовании в экономических задачах модели ARMA (p, q), потребностям практики, как правило, удовлетворяют следующие пять видов этой модели, представленных в таблице.

Свойства автокорреляционных (АКФ)

и частных автокорреляционных (ЧАКФ) функций

Функ- ция	ARMA(1,0)	ARMA(2,0)	ARMA(0,1)	ARMA(0,2)	ARMA(1,1)
АКФ	Экспоненциально затухает (монотон-но или знакопе-ременно)	Экспонен-циально затухает или имеет форму синусои-дальной волны	Выброс (пик) на лаге 1	Выбросы (пики) на лагах 1 и 2	Экспоненциально затухает от значения r (1) (монотонно или знако-переменно)
ЧАКФ	Выброс (пик) на лаге 1	Выбросы (пики) на лагах 1 и 2	Экспонен-циально затухает (монотон-но или знако-переменно)	Экспонен-циально затухает или имеет форму синусоидальной волны	Экспоненциально убывает от значения rч (1) (монотонно или знако-переменно)

В этой таблице указаны свойства АКФ и ЧАКФ для этих моделей. Очевидно, что модели ARMA (1,0) и ARMA (2,0) — это рассмотренные ранее модели AR (1), AR (2), а модели ARMA (0,1) и ARMA (0,2) соответствуют моделям скользящего среднего МА (1) и МА (2).