Трендовые модели прогнозирования экономических процессов

В практике прогнозирования и планирования показате­лей хозяйственной деятельности торговых предприятий мо­гут применяться различные виды экономико-статистичес­ких моделей. Основой большинства из них является экстра­поляция, связанная с распространением закономерностей, связей и соотношений, действующих в изучаемом периоде, за его пределы. В более широком смысле слова — это получе­ние представлений о будущем на основе информации, отно­сящейся к прошлому и настоящему.

В краткосрочном периоде прогнозирова­ния на экономический объект действует немало случайных факторов, ослабляющих определяющие тенденции его раз­вития. Поэтому использование экстраполяции в прогнозиро­вании имеет в своей основе предположение о том, что рас­сматриваемый процесс изменения той или иной экономичес­кой переменной представляет собой сочетание двух состав­ляющих — x_t регулярной (детерминированной неслучайной) и ε_t случайной. Тогда временной ряд экономического показа­теля y_t может быть представлен в следующем виде: y_t = x_t + ε_t.

Регулярная составляющая называется тенденцией, трен­дом. Регулярная составляю­щая (тренд) x_t характеризует существующую динамику раз­вития процесса в целом, случайная составляющая ε_t отража­ет случайные колебания или шумы процесса. Обе составляю­щие определяются каким-либо функциональным механиз­мом, характеризующим их поведение во времени. Задача прогноза состоит в определении вида экстраполирующей функции x_t и ε_t (на основе исходных эмпирических данных) и параметров выбранной функции.

Методика построения и виды моделей тренда

Расчет прогноза экономического показателя на основе его временного ряда является наиболее простым и распрос­траненным способом экстраполяционного прогнозирования. Цель такого прогноза — показать, к каким результатам можно прийти в будущем, если двигаться к нему с той же скоростью или ускорением, что и в прошлом.

В основе построения моделей тренда лежит предположе­ние, что прогнозируемый показатель формируется под воз­действием большого количества факторов, которые либо не­возможно выделить, либо по ним отсутствует информация. В этом случае ход изменения исследуемой переменной связы­вают не с факторами, а с течением времени, что проявляется в образовании одномерного временного ряда. Тогда формаль­но задача прогнозирования сводится к получению оценок значения ряда на некотором периоде будущего, т.е. к получе­нию значения y_t, где t = n + 1, n + 2 и т.д.

Прогнозные расчеты на основе трендовых моделей стро­ятся в два этапа. На первом (формальном) — выявляют при помощи статистических методов закономерности прошлого развития и переносят (экстраполируют) их на некоторый пе­риод будущего. На втором — производится корректировка полученного прогноза с учетом результатов содержательного анализа текущего состояния и действия экономического ме­ханизма на период прогнозирования.

В процессе формального этапа при моделировании эконо­мической динамики осуществляют следующие основные опе­рации:

1) сглаживание (выравнивание) исходного ряда в целях более четкого выявления тенденции развития исследуемого процесса (методом скользящего среднего, экспоненциально­го сглаживания и др.);

2) определение наличия тренда, т.е. изменения, опреде­ляющего общее направление развития, основную тенденцию временного ряда (на основе графического метода, использо­вания аппарата теории вероятностей и математической ста­тистики);

3) отбор одной или нескольких кривых роста;

4) определение их параметров;

5) оценку адекватности и точности трендовых моделей по критериям серий, пиков, на основе исследования показате­лей асимметрии и эксцесса, t -критерия Стьюдента, d -критерия Дарбина-Уотсона, среднего квадратического отклоне­ния, относительной ошибки аппроксимации, коэффициента сходимости и др.

При выравнивании временных рядов необходимо решать вопрос о том, какой длины должен быть ряд, выбираемый для прогнозирования. С одной стороны, если период ряда слишком короткий, можно не обнаружить тенденцию его развития. С другой стороны, очень длинный временной ряд может охватывать периоды с различными трендами, и его описание с помощью одной кривой роста не даст положи­тельных результатов. Поэтому следует придерживаться сле­дующих правил.

Если нет никаких соображений качествен­ного порядка, следует брать возможно больший промежуток времени. Если развитие обнаруживает циклический харак­тер, следует брать период от середины первого до середины последнего периода цикла. Если ряд охватывает периоды с разными трендами, лучше сократить ряд, отбросив наиболее ранние уровни, которые относятся к периоду с иной тенден­цией развития.

Модель тренда может иметь различный вид. Ее выбор в каждом конкретном случае осуществляется по целому ряду статистических критериев. Наибольшее распространение при построении трендовых моделей экономических процессов получили полиномиальные, экспоненциальные и S-образные кривые роста.

Простейшие полиномиальные кривые роста имеют вид:

y_t = b+ m₁t (полином первой степени);

y_t = b + m₁t + m₂t² (полином второй степени);

y_t = b + m₁t + m₂t² + m₃t³ (полином третьей степени) и т.д.

Такие кривые роста можно использовать для аппрокси­мации (приближения) и прогнозирования экономических процессов, в которых последующее развитие не зависит от достигнутого уровня.

В отличие от этого использование экспоненциальных кривых роста предполагает, что дальнейшее развитие зави­сит от достигнутого уровня (например, прирост зависит от значения функции).

В экономических расчетах чаще всего применяют две разновидности экспоненциальных (показа­тельных) кривых:

1) простая экспонента вида y_t = b m^t;

2) модифицированная экспонента вида y_t = а + b m^t.

В экономике достаточно часто встречаются процессы, ко­торые сначала растут медленно, затем ускоряются, а затем снова замедляют свой рост, стремясь к какому-либо пределу. Такой тип развития характерен, например, для спроса на не­которые новые товары. Для моделирования подобных про­цессов используют S-образные кривые роста, среди кото­рых выделяют кривую Гомперца (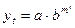) и логистическую кривую ().

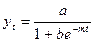На практике при предварительном отборе выбирают обыч­но 2-3 кривые роста для дальнейшего исследования и постро­ения трендовой модели рассматриваемого временного ряда.

Параметры приведенных трендовых моделей могут быть содержательно интерпретированы. Так, параметр b в поли­номиальных кривых роста задает начальные уровни разви­тия, параметр m₁ определяет скорость или интенсивность развития, параметр m₂ — изменение скорости или интенсив­ности развития.

Добавление линии тренда к рядам данных на диаграмме. Если имеется некоторая совокупность данных, характе­ризующих динамику исследуемого показателя, то всегда можно попытаться найти на графике наилучшую линию, ко­торая будет «ближайшей» к точкам наблюдений в рамках всей их совокупности. Эта линия поможет понять поведение фактических данных, выявить тенденцию их развития и на этой основе построить оптимальный прогноз будущих значений ряда. Использование графического метода в сочетании с возможностями Excel позволяет не только оперативно пос­троить линию, наилучшим образом аппроксимирующую ис­ходные данные, но и дать ей математическое описание и ка­чественную оценку.

Добавление линий тренда к рядам данных на диаграмме является весьма простым, наглядным и быстрым способом составления и оценки достоверности прогнозов. Преимущес­тво этого способа прогнозирования состоит в том, что однов­ременно можно получить сразу несколько кривых роста, в той или иной степени отражающих поведение базовой линии и построенных на основе различных моделей. Тем самым расширяется аналитическая база прогнозирования, и поль­зователь получает больше аргументов для содержательной оценки возможных направлений развития исследуемого по­казателя.

При необходимости сформиро­ванная база прогнозных величин может быть дополнена изу­чением степени влияния на развитие исследуемого показате­ля тех или иных факторов, находящихся с ним в непосред­ственной взаимосвязи. В этом случае окончательный вари­ант прогноза будет формироваться с учетом размеров и нап­равлений возможного изменения факторов, оказывающих существенное влияние на исследуемый показатель.

Прогнозирование с применением функции экспоненциального сглаживания. Сглаживание представляет собой метод, который обеспе­чивает быструю реакцию значений прогноза на все процес­сы, происходящие в рамках данных базового ряда.

Основная идея применения метода сглаживания состоит в том, что каждый новый прогноз получается посредством перемещения предыдущего прогноза в направлении, обеспе­чивающем лучший результат по сравнению со старым прогно­зом. По сути этот метод позволяет строить самокорректирую­щиеся модели, которые, учитывая результат прогноза, сде­ланного на предыдущем шаге, и различную информационную ценность членов динамического ряда, способны оперативно реагировать на изменяющиеся условия и на этой основе да­вать на ближайшую перспективу более точные прогнозы.

Моде­ли, построенные с помощью метода экспоненциального сгла­живания, достаточно гибки и более точно отражают динами­ку исследуемого показателя, учитывая эффекты выброса функции намного лучше моделей, построенных с примене­нием метода наименьших квадратов. Однако нельзя рассчи­тывать на их универсальность и пригодность для любого на­бора данных и периода упреждения. Так, инструмент Экспо­ненциальное сглаживание целесообразно применять для со­ставления прогнозов только на период, непосредственно сле­дующий за интервалом базовых наблюдений. Кроме того, при построении модели, описывающей поведение динамиче­ского ряда конкретного показателя, важно правильно оце­нить наиболее вероятные закономерности его развития в бу­дущем. Закладывать в модель следует те адаптивные свойст­ва, которых достаточно, чтобы с заданной точностью отсле­дить динамику реального процесса.

Значи­тельно упростить и ускорить процедуру прогнозирования ис­следуемого показателя позволяет Microsoft Excel, который предлагает три основных подхода к этому процессу: приме­нение скользящего среднего, вычисление линейных и нели­нейных прогнозов с помощью соответствующих функций ра­бочего листа и использование метода сглаживания.

Вычисление скользящего среднего средствами Excel. Расчет скользящего среднего — это, прежде всего, метод, который позволяет упростить определение и анализ тенден­ции в развитии динамического ряда на основе сглаживания колебаний измерений по временным интервалам.

Сглаживание колебаний динамического ряда предпола­гает вычисление новых данных, каждое из которых пред­ставляет собой средний показатель нескольких результатов наблюдений первоначального (базового) ряда. Для их опре­деления важно правильно задать интервал усреднения: при малом интервале вновь созданный динамический ряд может не отразить тенденцию, а при большом — слишком сгладит ее. Если, например, интервал усреднения принять равным трем, то первое значение нового ряда, создаваемого методом скользящего среднего, — это среднее значение первых трех периодов первоначального ряда; следующее значение - сред­нее со второго по четвертый период и т.д.

Метод скользящего среднего довольно прост в примене­нии, а полученные на его основе результаты достаточно точ­но отражают общую тенденцию поведения исследуемых по­казателей базового ряда. Однако по мере увеличения количе­ства членов первоначального динамического ряда возраста­ют и затраты времени на их математическую обработку и анализ. Облегчить и ускорить процедуру расчетов помогает инструмент MS Excel Скользящее среднее.

Инструмент Скользящее среднее можно также использо­вать при составлении прогнозов экономических показате­лей. Как правило, прогноз с применением скользящего сред­него составляется на период, непосредственно следующий за интервалом наблюдения. Для этого на основе вновь рассчи­танных (сглаженных с помощью скользящего среднего) величин динамического ряда определяют среднее изменение исследуемого показателя (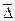) по формуле

,

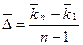где 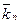— последний член выровненного ряда;

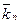— первый член вы­ровненного ряда;

n — количество членов выровненного ряда.

Тогда прогнозируемая величина исследуемого показателя (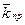) рассчитывается путем суммирования последнего члена выровненного ряда и удвоенной величины :

.

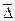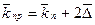С целью обеспечения корректности прогноза и снижения погрешности вычислений при использовании скользящего среднего исходный динамический ряд целесообразно по воз­можности формировать на основе натуральных или относи­тельных (для стоимостных показателей) величин. Примером последних могут быть темпы прироста (для объемных пока­зателей — товарооборота, суммы валовых доходов, суммы издержек обращения, суммы прибыли и т.д.), уровни, удельные веса и т.д.

Расчет скользящего среднего является быстрым и про­стым способом краткосрочного прогнозирования экономи­ческих показателей.

Составление линейных и нелинейных прогнозов средствами Excel. По типу функциональных зависимостей экзогенных пе­ременных модели тренда могут быть линейными и нелиней­ными. Сложность экономических процессов и свойство от­крытости экономических систем обусловливают в большин­стве случаев нелинейный характер развития экономических показателей. Однако построение линейных моделей являет­ся гораздо менее трудоемкой и с технической, и с математи­ческой точек зрения процедурой. Поэтому на практике не­редко допускают частичное преобразование нелинейных про­цессов (при условии, что предварительно проведенный гра­фический анализ данных позволяет это сделать), и модели­рование поведения исследуемого показателя сводится к со­ставлению и оценке линейного уравнения его динамики.

Функции ЛИНЕЙН, ТЕНДЕНЦИЯ, ПРЕДСКАЗ помога­ют пользователю составить прогнозы, основанные на линей­ной связи между результатом наблюдения и временем, когда этот результат был зафиксирован (или в течение которого на­капливался). Их использование возможно в тех случаях, ко­гда предварительно проведенный графический анализ базо­вых данных показывает, что точки наблюдений группируют­ся вокруг некоторой прямой линии.

Если же эта линия начи­нает резко изгибаться в одном из направлений, то пользова­тель имеет дело с данными, которые изменяются во времени нелинейным образом. В этом случае более точную картину динамики исследуемого показателя помогут получить функ­ции Excel ЛГРФПРИБЛ и РОСТ, в основе которых лежит уравнение экспоненци­альной кривой вида

у = b × m^x (или у = b × m^х),

где х = t — временной тренд (порядковый номер периода); b, т — параметры уравнения; значение т является основанием для возве­дения в степень х, а значение b — постоянно.