Суть методу в наступному: якщо підінтегральна функція представима у виді добутку двох неперервних і повних функцій (кожна з який може бути як елементарною функцією, так і композицією), то справедливі формули
для невизначеного інтеграла:
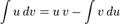
для визначеного:
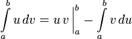
Передбачається, що знаходження інтеграла 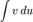 простіше, ніж
простіше, ніж 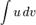 . У іншому випадку застосування методу не виправдано.
. У іншому випадку застосування методу не виправдано.
Одержання формул
Для невизначеного інтеграла
Функції 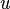 и
и  повні, отже, можливе диференціювання:
повні, отже, можливе диференціювання:
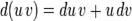
Ці функції також неперервні, значить можна взяти інтеграл від обох частин рівності:
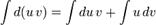
Операція інтегрування протилежна диференціюванню:
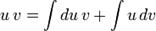
Після перестановок: 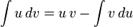
 2015-09-07
2015-09-07 255
255








