Учение о пропорциях

Характерной особенностью пифагорейского мышления было не просто стремление все измерять, постигая вещи при помощи чисел, но и соизмерять, т. е. сравнивать измеренные величины и тем самым раскрывать внутренние связи между ними. Вот почему пропорции, т. е. равенства отношений, стали изучаться пифагорейцами раньше, чем сами отношения. К этому побуждала не только пифагорейская философия «извлечения числа из вещей», но и сама жизнь и прежде всего искусство архитектуры, где пропорции во все времена играли заглавную роль. И только впоследствии из учения о пропорциях родилось учение об отношениях, вершиной которого стала общая теория отношений Евдокса[40] (ок. 408 — ок. 355) —одно из высочайших достижений греческой математики.

Слово «пропорция» ввел в употребление в I в. до н. э. Цицерон, переведя им на латынь греческий термин «аналогия», который буквально означал «вновь отношение», или, как мы говорим, соотношение. С тех пор вот уже 2000 лет пропорцией в математике называют равенство между двумя отношениями четырех величин — a, b, c, d:

причем величины 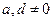называют крайними членами пропорции, а величины 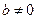и c — средними.

Сегодня, когда известны рациональные и иррациональные числа, это определение кажется тривиальным, ибо всякое отношение двух величин может быть представлено рациональным или иррациональным числом. Сегодня, когда законы арифметических операций, установленные для натуральных чисел, распространены и на другие множества чисел вплоть до иррациональных, нет никакой необходимости создавать специальные правила действия с отношениями, а само равенство отношений легко перевести в равенство произведений, именуемое основным свойством пропорции: произведение средних членов пропорции равно произведению ее крайних членов:

Совсем в иной ситуации находился древнегреческий математик. Как следовало ему понимать отношение величин 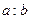? Хорошо, если меньшая величина b целое число раз m укладывалась в большей a, т. е. 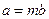. Тогда отношением величин 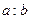можно было бы назвать число m, т. е. 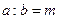. Однако так было далеко не всегда, и вот тут-то для греческого математика, знавшего только натуральные числа, возникали серьезные трудности.

Мы не знаем, как преодолевали эти трудности ранние пифагорейцы, хотя известно, что они широко пользовались пропорциями. (Вспомним, что еще Фалес, измеряя высоту пирамиды по длине ее тени и высоте и длине тени шеста, фактически пользовался пропорцией.) Но нам доподлинно известно, что в трудах друзей Платона Теэтета (? — 369 до н. э.) и Архита была построена теория отношений для соизмеримых величин (целых чисел), которую затем обобщил на случай несоизмеримых величин ученик Архита Евдокс. Все эти теории вошли в «Начала» Евклида, откуда мы их и знаем. Считается, что V книга «Начал» принадлежит Евдоксу, VII — Теэтету, а VIII — Архиту.

Итак, дробь как число для пифагорейцев не существовала, поскольку единица («числовой атом») считалась ими неделимой.

Поэтому дробь 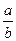понималась не как доля единицы — 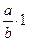, а как отношение двух целых чисел 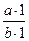. Согласно VII книге «Начал», отношения 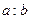и 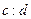назывались равными, если у a и b существовал такой общий делитель p, а у c и d — делитель q, что

(в частности, при 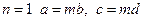). Тогда пары целых чисел разбивались на непересекающиеся классы пар, имеющих одинаковые отношения:

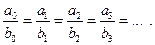
Именно такие классы пропорциональных пар и дают любые две строки таблицы Пифагора. Далее в «Началах» доказывалось, что наименьшая пара 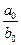— полностью определяет свой класс. Сегодня эту пару (несократимую дробь) мы бы назвали рациональным числом, определяющим данный класс.

В основе большей части доказательств теории отношений лежал универсальный способ нахождения наибольшего общего делителя двух чисел. Этот способ и сегодня с успехом применяется в теории чисел и называется алгоритмом Евклида. Суть алгоритма Евклида состоит в том, что a делят на b с остатком, затем b делят на этот остаток и т. д.

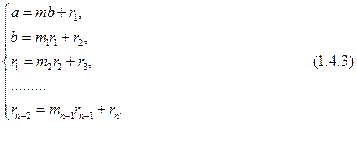
Евклид доказал, что:

1) если 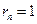, то 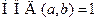, т.е. числа a и b взаимно простые;

2) если 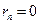, то 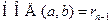. Записывая систему равенства (1.4.3) в виде

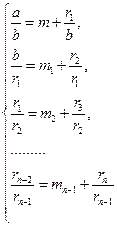
и подставляя последующие равенства в предыдущие, получим

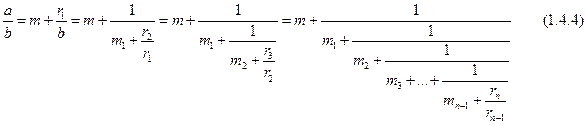
Дробь (1.4.4) называется непрерывной. Из самого принципа построения непрерывной дроби видно, что если она конечна, то, значит, числа a и b имеют общую меру, т. е. число 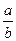является рациональным. Бесконечная непрерывная дробь будет получаться в случае, если a и b несоизмеримы, т. е. когда число 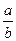иррациональное. Таким образом, непрерывная дробь является прекрасным критерием рациональности или иррациональности числа. Однако переход от алгоритма Евклида к непрерывным дробям был осуществлен только через 2000 лет, в эпоху Возрождения.

Стремясь обобщить теорию отношений на несоизмеримые величины, Евдокс вводит новое определение величины. Это определение включало в себя как числа, так и любые непрерывные величины (отрезки, площади), в том числе и несоизмеримые. Понятие величины определялось с помощью аксиом равенства и неравенства, и в частности двумя знаменитыми аксиомами.

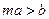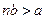1. «Говорят, что величины имеют отношение между собой, если они, взятые кратно, могут превзойти друг друга» («Начала», кн. V, опред. 4). Иначе, для любых a и b существуют такие числа m и n, что и . Эта аксиома известна в математике как аксиома Архимеда, а величины a и b, для которых она выполняется, называются архимедовыми.

2. «Говорят, что величины находятся в том же отношении первая ко второй и третья к четвертой, если равнократные первой и третьей одновременно больше, или одновременно равны, или одновременно меньше равнократных второй и четвертой каждая каждой при какой бы то ни было кратности, если взять их в соответственном порядке» («Начала», кн. V, опред. 5). Иначе, 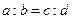, если для любых m и n справедливо одно из утверждений:

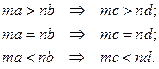
Эта аксиома, ставшая через 23 века отправным пунктом современной теории действительных чисел, позволяла сравнивать отношения несоизмеримых величин. Оставалось только назвать отношение 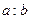числом (рациональным, если a и b имели общую меру, и иррациональным в противном случае). Однако это сделал только Ньютон в своей «Всеобщей арифметике» в 1707 г.: «Под числами мы понимаем не столько множество единиц, сколько отвлеченное отношение какой-нибудь величины к другой величине того же рода, принятой нами за единицу».

Истинная же глубина теории Евдокса была до конца осознана лишь во второй половине XIX в., после того как немецкий математик Рихард Дедекинд (1831 — 1916) построил теорию действительного числа как сечения во множестве рациональных чисел. Вторая аксиома Евдокса, по существу, стала отправным пунктом теории Дедекинда, которая настолько близко следовала ходу мыслей Евдокса, что это дало повод его соотечественнику Р. Липшицу в одном из писем спросить Дедекинда, что же он сделал нового по сравнению с Евдоксом. В это же время еще один выдающийся немецкий математик Феликс Клейн (1849 — 1925) назвал теорию отношений Евдокса одним из перлов античной математической мысли.

Но вернемся к пропорциям. Традиция утверждает, что древние пифагорейцы знали три вида пропорций:

арифметическая: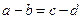

геометрическая: 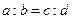(1.4.5)

гармоническая: .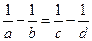

Помимо обычных пропорций пифагорейцы особое внимание уделяли непрерывным пропорциям, или средним величинам, т. е. таким пропорциям, у которых средние члены совпадали (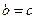). Пифагорейцы не только изучали математические свойства средних, но и наполняли их глубоким эстетическим содержанием. Об этом красноречиво свидетельствует следующий отрывок из платоновского «Тимея»: «Невозможно, чтобы две вещи совершенным образом соединились без третьей, так как между ними должна появиться связь, которая скрепила бы их. Это наилучшим образом может выполнить пропорция...»

Полагая в (1.4.5) 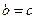и переобозначая d через c, получим следующие выражения для средних:

арифметическое среднее: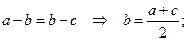

геометрическое среднее: 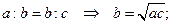(1.4.6)

гармоническое среднее: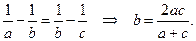

Арифметическое среднее понималось пифагорейцами арифметически: как отрезок b, меньший большего отрезка a и больший меньшего c на одну и ту же величину 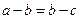. Геометрическое среднее (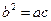) — геометрически: как площадь квадрата со стороной b, равновеликого прямоугольнику со сторонами a и c. Наконец, гармоническое среднее — как арифметическое среднее для обратных величин. Гармоническое среднее играло большую роль в пифагорейской теории музыки — гармонии, откуда и происходит его название.

Среди бесчисленного множества геометрических средних уникальными свойствами обладает одно, делящее данный отрезок a на две части x и 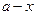в геометрической пропорции, т. е. так, что отношение целого отрезка a к его большей части x равняется отношению большей части x к меньшей :

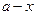Эта геометрическая пропорция приводит к уравнению

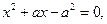
которое имеет один положительный корень:

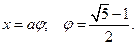
Заметим, что 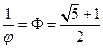, т. е. 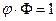, причем

φ = 0,618033988...;

Ф = 1,618033988....

Найдем разложение φ в непрерывную дробь. Рассмотрим бесконечную непрерывную дробь:

в знаменателе которой нетрудно обнаружить выражение 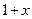, т. е.

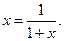
Отсюда находим уравнение

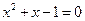
и его положительный корень 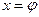. Следовательно, дробь (1.4.8) и есть искомое разложение для φ.

Уже этих двух свойств достаточно для того, чтобы заметить в пропорции (1.4.7) нечто поистине уникальное. Вот почему эта удивительная пропорция, известная со времен древних пифагорейцев, в эпоху Возрождения была названа ее страстным почитателем и неутомимым исследователем Леонардо да Винчи (1452 — 1519) золотым сечением. Но, несмотря на более чем двухтысячелетнюю историю, золотое сечение и сегодня раскрыло далеко не все свои тайны. Помимо массы интереснейших математических свойств золотое сечение имеет множество подчас загадочных проявлений как в природе, так и в искусстве. С некоторыми из этих свойств, выходящих за рамки нашего повествования, можно познакомиться, например, в книге Н. Васютинского «Золотая пропорция» (М.: Молодая гвардия, 1990).

А сейчас мы ограничимся лишь оценкой золотого сечения, данной более 300 лет назад выдающимся немецким математиком и астрономам Иоганном Кеплером: «Геометрия владеет двумя сокровищами: одно из них — это теорема Пифагора, а другое — деление отрезка в среднем и крайнем отношении... Первое можно сравнить с мерой золота; второе же больше напоминает драгоценный камень.

Отметим одно любопытное свойство всех трех средних величин, которое, как утверждает Ямвлих во «Введении в никомахову арифметику», Пифагор привез из Вавилона. Пусть даны две величины 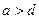. Составим их среднее арифметическое 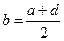и среднее гармоническое 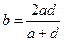. Легко показать, что :

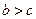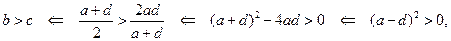
т. е. 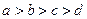. Кроме того, легко видеть, что

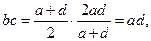
т. е. выполняется основное свойство пропорции (1.4.2), и, следовательно, среднее арифметическое и среднее гармоническое двух величин a и d образуют с ними геометрическую пропорцию:

Эта пропорция играла значительную роль в пифагорейской теории музыки, отчего ее часто называют музыкальной.

Знакомясь с пифагорейским учением, мы не раз еще встретимся с музыкальной пропорцией и со всеми видами средних. Пропорции помогали пифагорейцам «извлекать числа из вещей» и щедро раскрывали перед ними свои сокровища. Возможно, что именно изучение геометрической пропорции и геометрической средней привело пифагорейцев к их главному и трагическому открытию — открытию несоизмеримости.