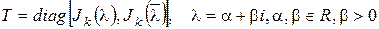 подобна над полем
подобна над полем 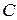 матрице
матрице 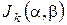 .
.
Доказательство. Пусть 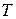 — матрица линейного оператора
— матрица линейного оператора 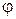
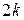 -мерного комплексного пространства
-мерного комплексного пространства 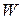 в базисе
в базисе 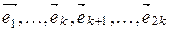 (1).
(1).
Рассмотрим систему векторов
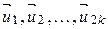 (2)
(2)
где 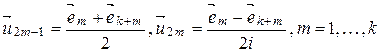 .
.
Покажем, что (2) — линейно независимая система.
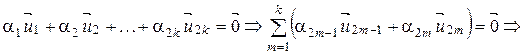
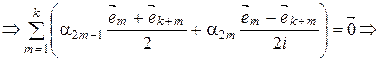
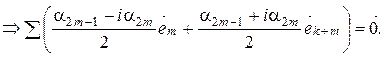
Так как (I) – базис 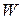 , то
, то 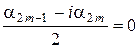 и
и 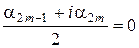 , т.е.
, т.е. 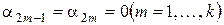 . Так как (2) линейно независима и содержит
. Так как (2) линейно независима и содержит 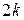 векторов, то (2) – базис
векторов, то (2) – базис  .
.
Найдем матрицу  в базисе (2).
в базисе (2).
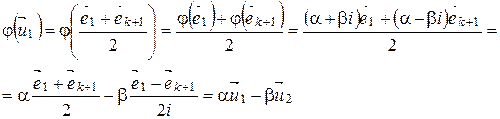
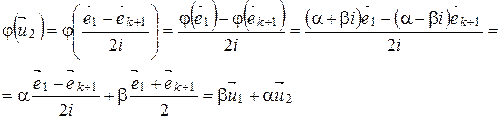
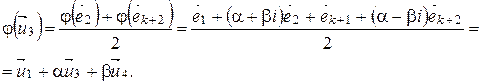
 .
.
……………………….
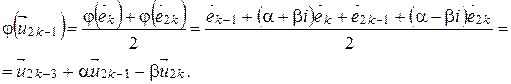
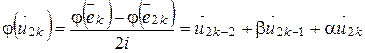 .
.
Следовательно, матрица  в базисе (2) равна
в базисе (2) равна
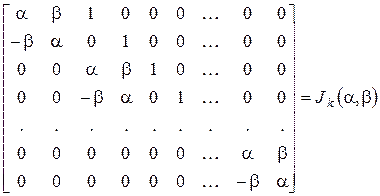 .
.
Так как  и
и  матрицы одного линейного оператора в базисах (I) и (2) соответственно, то они подобны.
матрицы одного линейного оператора в базисах (I) и (2) соответственно, то они подобны.
Упражнение. Пусть 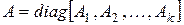 ,
,
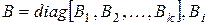 подобна
подобна 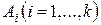 . Тогда матрица
. Тогда матрица 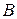 подобна матрице
подобна матрице  .
.
Лемма 3. Всякая действительная квадратная матрица подобна над полем 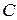 обобщенной жордановой матрице.
обобщенной жордановой матрице.
Доказательство. Пусть 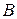 действительная квадратная матрица. Снова доказательства требует лишь случай, когда характеристический полином матрицы
действительная квадратная матрица. Снова доказательства требует лишь случай, когда характеристический полином матрицы 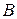 имеет недействительные корни. В этом случае жорданова нормальная форма
имеет недействительные корни. В этом случае жорданова нормальная форма 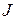 матрицы
матрицы 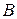 над полем
над полем 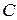 в силу леммы I имеет вид
в силу леммы I имеет вид
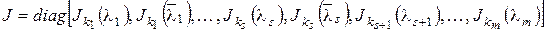 , где
, где 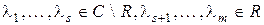 .
.
Если 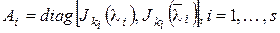 , то
, то 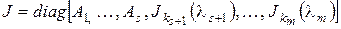 . По лемме 2
. По лемме 2 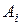 подобна над полем
подобна над полем  обобщенной клетке Жордана. Следовательно, матрица
обобщенной клетке Жордана. Следовательно, матрица 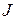 подобна над полем
подобна над полем 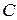 обобщенной матрице Жордана.
обобщенной матрице Жордана.
Лемма 4. Если действительные матрицы подобны над полем комплексных чисел, то они подобны и над полем действительных чисел.
Доказательство. Пусть  и
и 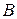 — действительные квадратные матрицы, подобные над полем
— действительные квадратные матрицы, подобные над полем 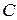 . Нужно доказать существование действительной матрицы
. Нужно доказать существование действительной матрицы 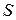 такой, что
такой, что
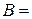
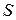 -1
-1 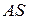 (I)
(I)
Умножим слева обе части равенства (I) на 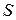 и перенесем все члены в одну сторону. Получим равенство
и перенесем все члены в одну сторону. Получим равенство
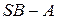
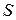
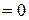 (2)
(2)
которое можно рассматривать как однородную систему линейных уравнений, в которой неизвестными являются элементы матрицы 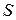 . Любое решение такой системы, удовлетворяющее дополнительному условию
. Любое решение такой системы, удовлетворяющее дополнительному условию
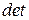
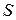
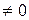
дает нужную матрицу 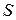 .
.
Так как матрицы  и
и 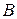 подобны над полем
подобны над полем 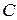 , то (2) имеет ненулевые комплексные решения. В силу того, что к тому же коэффициенты при неизвестных в (2) действительны, система (2) имеет ненулевые действительные решения.
, то (2) имеет ненулевые комплексные решения. В силу того, что к тому же коэффициенты при неизвестных в (2) действительны, система (2) имеет ненулевые действительные решения.
Пусть 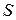
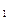 ,
, 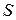
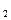 ,…,
,…, 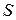
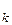 — фундаментальная система
— фундаментальная система
действительных решений системы (2). Тогда всякое действительное решение системы (2) имеет вид
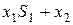
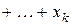
 , где
, где 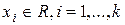 . Нужно показать, что существуют действительные значения
. Нужно показать, что существуют действительные значения 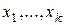 такие, что
такие, что 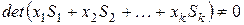 .
.
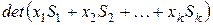 является, очевидно, полиномом с действительными коэффициентами от неизвестных
является, очевидно, полиномом с действительными коэффициентами от неизвестных 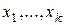 . Обозначим его через
. Обозначим его через 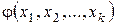 .
. 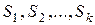 является также фундаментальной системой решений системы (2), рассматриваемой над полем комплексных чисел. Так как матрицы
является также фундаментальной системой решений системы (2), рассматриваемой над полем комплексных чисел. Так как матрицы  и
и 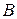 подобны над этим полем, то существуют комплексные значения
подобны над этим полем, то существуют комплексные значения 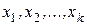 такие, что
такие, что 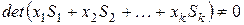 , т.е. полином
, т.е. полином 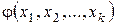 - ненулевой.
- ненулевой.
Методом математической индукции по количеству неизвестных легко доказывается, что для ненулевого полинома с действительными коэффициентами от нескольких неизвестных существует точка, в которой он принимает ненулевое значение.
Лемма доказана.
Из леммы 3,4 и теоремы 8 вытекает доказываемая нами теорема 9.
Приведем теперь алгоритм построения обобщенной жордановой нормальной формы 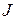 матрицы, вытекающий из доказательства теоремы 9.
матрицы, вытекающий из доказательства теоремы 9.
1. Находим характеристический полином 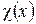 матрицы и его корни. Из множества всех корней этого полинома выделим все различные корни с нетрицательной мнимой частью.
матрицы и его корни. Из множества всех корней этого полинома выделим все различные корни с нетрицательной мнимой частью.
2. Пусть 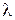 — один из выделенных корней. При этом в случае вещественного
— один из выделенных корней. При этом в случае вещественного 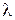 , пользуясь формулами (*) и (**) предыдущего параграфа, находим все клетки Жордана матрицы
, пользуясь формулами (*) и (**) предыдущего параграфа, находим все клетки Жордана матрицы 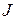 с чилом
с чилом 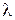 на диагонали. Если же
на диагонали. Если же 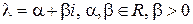 , то пишем
, то пишем 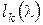 клеток
клеток 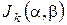 для каждого из возможных значений
для каждого из возможных значений 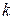 .
.
3. Переходим к следующему из выделенных корней. С ним поступаем также, как и с 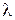 . Процесс заканчивается, когда переберем все выделенные на первом шаге корни.
. Процесс заканчивается, когда переберем все выделенные на первом шаге корни.
4. Из всех полученных клеток Жордана и обобщенных клеток Жордана составляем квазидиагональную матрицу. Эта матрица – искомая.
Замечание. При решении конкретных примеров целесообразно использовать соображения, высказанные ранее при построении жордановой нормальной формы.
Пример 1. Найти обобщенную жорданову нормальную форму матрицы 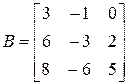
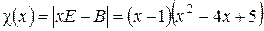 .
.
Корни 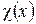 таковы:
таковы: 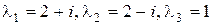 . Следовательно,
. Следовательно,
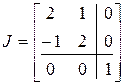 .
.
Пример 2. 
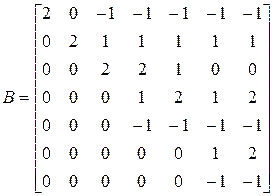 .
.
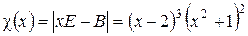 .
.
Корни 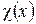 с неотрицательной мнимой частью таковы:
с неотрицательной мнимой частью таковы: 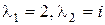 . Так как кратность каждого их них не выше
. Так как кратность каждого их них не выше 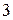 , то для построения обобщенной жордановой формы достаточно найти количество всех клеток Жордана матрицы
, то для построения обобщенной жордановой формы достаточно найти количество всех клеток Жордана матрицы 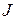 с числами
с числами 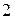 и
и 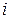 на диагонали, т.е. нужно найти
на диагонали, т.е. нужно найти 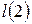 и
и 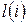 .
.
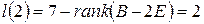 .
.
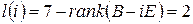 .
.
Следовательно,
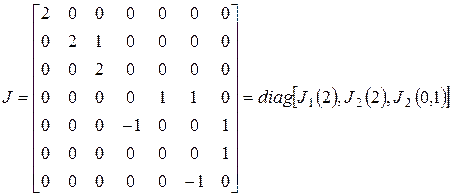 .
.
§ 6. Нормальная форма Фробениуса.
Пусть  — произвольное поле, а
— произвольное поле, а
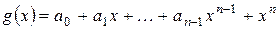 - многочлен ненулевой степени
- многочлен ненулевой степени 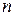 над полем
над полем 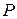 . Матрица
. Матрица
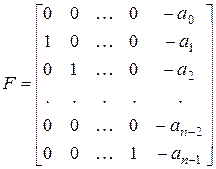
называется клеткой Фробениуса, сопровождающей многочлен 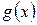 . Например,
. Например,
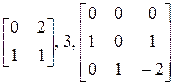 -
-
клетки Фробениуса, сопровождающие соответственно многочлены 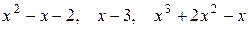 . Пусть
. Пусть
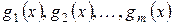 (I)
(I)
такая система многочленов ненулевых степеней над полем 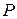 , что для
, что для 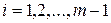 многочлен
многочлен 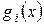 делит многочлен
делит многочлен 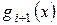 и старший коэффициент каждого из них равен I. Пусть, далее,
и старший коэффициент каждого из них равен I. Пусть, далее, 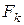 - клетка
- клетка
Фробениуса, сопровождающая многочлен 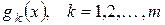 .
.
Квазидиагональная матрица 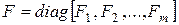 называется матрицей Фробениуса, сопровождающей систему многочленов (I).
называется матрицей Фробениуса, сопровождающей систему многочленов (I).
Если  — матрица, а
— матрица, а 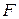 — подобная ей матрица Фробениуса, то
— подобная ей матрица Фробениуса, то 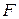 называется нормальной формой Фробениуса матрицы
называется нормальной формой Фробениуса матрицы  .
.
Пусть 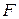 — клетка Фробениуса, сопровождающая многочлен
— клетка Фробениуса, сопровождающая многочлен 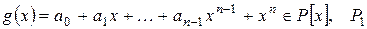 - расширение поля
- расширение поля 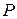 , содержащее все корни многочлена
, содержащее все корни многочлена 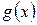 и
и 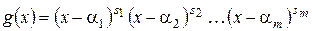 — каноническое разложение многочлена
— каноническое разложение многочлена 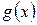 над полем
над полем 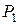 . Разлагая определитель
. Разлагая определитель
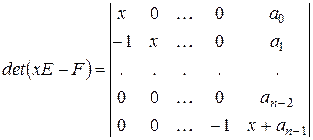
по элементам последнего столбца, получим 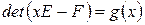 . Вычислим количество
. Вычислим количество 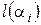 клеток Жордана с диагональным элементом
клеток Жордана с диагональным элементом 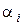 в жордановой нормальной форме матрицы
в жордановой нормальной форме матрицы 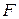 ,
, 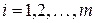 . С этой целью вычислим вначале ранг матрицы
. С этой целью вычислим вначале ранг матрицы 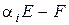 .
.
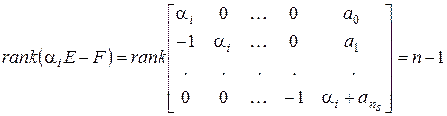 .
.
Следовательно, 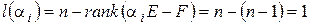 , и, значит, матрица
, и, значит, матрица
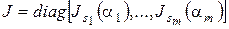
является жордановой нормальной формой матрицы 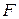 над полем
над полем 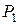 . Поэтому минимальный многочлен клетки Фробениуса
. Поэтому минимальный многочлен клетки Фробениуса 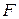 равен
равен 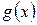 и, значит, минимальный многочлен матрицы Фробениуса, сопровождающей систему многочленов (1), равен
и, значит, минимальный многочлен матрицы Фробениуса, сопровождающей систему многочленов (1), равен 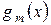 .
.
Пусть теперь  — произвольная матрица над полем
— произвольная матрица над полем 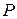 ,
, 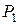 — расширение поля
— расширение поля 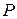 , содержащее все корни характеристического многочлена матрицы
, содержащее все корни характеристического многочлена матрицы  ,
,
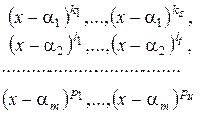 (2)
(2)
есть система ее элементарных делителей над полем 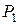
 . Будем считать многочлены в системе (2) расположенными так, что
. Будем считать многочлены в системе (2) расположенными так, что
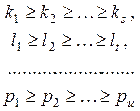 (3)
(3)
Пусть для определенности, первая цепочка неравенств (3) самая длинная, т.е. 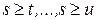 . Введя обозначения
. Введя обозначения 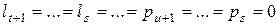 , получим неравенства
, получим неравенства

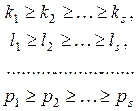 (4)
(4)
Рассмотрим многочлены
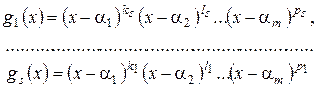 (5)
(5)
Заметим, что 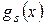 равен НОК системы (2).
равен НОК системы (2).
Упражнение. По аналогии с доказательством леммы I § 5 можно доказать, что коэффициенты многочленов 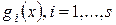 принадлежат полю
принадлежат полю 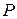 . Докажите.
. Докажите.
В силу неравенств (4) для каждого 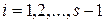 многочлен
многочлен 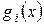 делит многочлен
делит многочлен 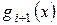 . Пусть
. Пусть 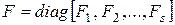 — матрица Фробениуса, сопровождающая систему многочленов (5). В силу того, что система элементарных делителей квазидиагональной матрицы является объединением систем элементарных делителей ее клеток, и только что рассмотренного случая, когда
— матрица Фробениуса, сопровождающая систему многочленов (5). В силу того, что система элементарных делителей квазидиагональной матрицы является объединением систем элементарных делителей ее клеток, и только что рассмотренного случая, когда 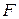 — клетка Фробениуса, системы элементарных делителей матриц
— клетка Фробениуса, системы элементарных делителей матриц  и
и 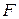 совпадают. Следовательно, матрицы
совпадают. Следовательно, матрицы  и
и 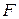 подобны над полем
подобны над полем 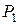 ,
, 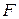 — нормальная форма Фробениуса матрицы
— нормальная форма Фробениуса матрицы  .
.
Упражнение. Доказать, что матрицы  и
и 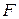 подобны над полем
подобны над полем 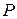 . (Для решения этого упражнения можно использовать идею доказательства леммы 4 § 5.)
. (Для решения этого упражнения можно использовать идею доказательства леммы 4 § 5.)
Докажем единственность нормальной формы Фробениуса матрицы  . Пусть еще
. Пусть еще 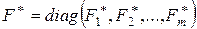 нормальная форма Фробениуса матрицы
нормальная форма Фробениуса матрицы  и
и 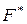 сопровождает систему многочленов
сопровождает систему многочленов 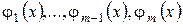 . Тогда
. Тогда 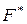 подобна
подобна 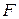 . Поэтому минимальные многочлены матриц
. Поэтому минимальные многочлены матриц 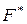 и
и 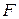 равны, т.е.
равны, т.е. 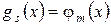 . Следовательно,
. Следовательно, 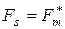 и, значит, системы элементарных делителей матриц
и, значит, системы элементарных делителей матриц 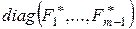 и
и 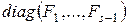 совпадают. Поэтому эти матрицы подобны. Проводя индукцию по числу
совпадают. Поэтому эти матрицы подобны. Проводя индукцию по числу 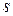 , теперь получаем
, теперь получаем 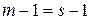 и
и 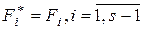 . Учитывая
. Учитывая 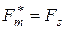 , получаем
, получаем 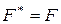 .
.
 2015-09-06
2015-09-06 1648
1648