Правило Лопіталя. Для “невизначеностей типу 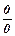 та
та 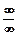 ” границя відношення функцій дорівнює границі відношення їх похідних, якщо вона існує.
” границя відношення функцій дорівнює границі відношення їх похідних, якщо вона існує.
Достатні умови зростання та спадання функції. Якщо похідна неперервної на відрізку 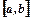 функції
функції 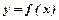 додатна, то функція зростає, якщо похідна – від’ємна, то функція спадна.
додатна, то функція зростає, якщо похідна – від’ємна, то функція спадна.
Необхідні умови екстремуму функції. Якщо в точці 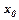 функція
функція 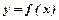 має екстремум, то її похідна
має екстремум, то її похідна 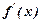 в цій точці дорівнює нулю або не існує.
в цій точці дорівнює нулю або не існує.
Точки, в яких похідна дорівнює нулю або не існує називають критичними.
Достатні умови екстремуму (перше правило).
Якщо при переході через критичну точку 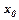 зліва на право похідна
зліва на право похідна 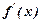 змінює знак з “+” на “-”, то в цій точці функція має максимум., а при зміні знака з “-” на “+” – мінімум. Якщо знак не міняється, то екстремуму не має.
змінює знак з “+” на “-”, то в цій точці функція має максимум., а при зміні знака з “-” на “+” – мінімум. Якщо знак не міняється, то екстремуму не має.
Друге правило.
Якщо в критичній точці 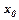 друга похідна
друга похідна 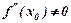 , то в цій точці функція
, то в цій точці функція 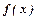 має екстремум: максимум при
має екстремум: максимум при 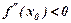 , мінімум при
, мінімум при 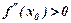 .
.
Графік функції 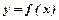 опуклий на проміжку
опуклий на проміжку 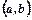 , якщо в кожній точці його
, якщо в кожній точці його 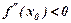 і вгнутий, якщо
і вгнутий, якщо 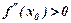 .
.
Точка 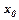 , в якій
, в якій 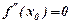 і при переході через яку
і при переході через яку 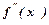 змінює знак є точкою перегину.
змінює знак є точкою перегину.
В економічних дослідженнях використовують поняття еластичності функції 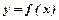 , яке виражається через похідну
, яке виражається через похідну
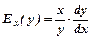 .
.
 2015-09-06
2015-09-06 495
495








