Якщо кожній парі чисел 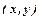 , де
, де 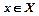 ,
, 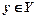 поставлено у відповідність за певним правилом значення
поставлено у відповідність за певним правилом значення 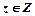 , то говорять, що задана функція двох змінних, яку позначають
, то говорять, що задана функція двох змінних, яку позначають 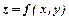 .
.
Змінні 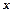 і
і 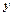 називають аргументами.
називають аргументами.
Якщо 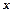 надати приросту
надати приросту 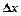 , а
, а 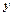 - приросту, то
- приросту, то 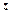 одержить приріст
одержить приріст 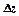 . Частинний приріст
. Частинний приріст 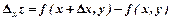 , частинний приріст
, частинний приріст 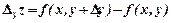 .
.
Частинні похідні першого порядку:
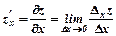 ,
, 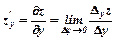 .
.
Їх знаходять як звичайні похідні, вважаючи при обчисленні 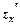 змінну
змінну 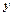 сталою, а при обчисленні
сталою, а при обчисленні 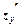 змінну
змінну 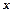 сталою. Оскільки частинні похідні першого порядку для функції двох змінних є функціями цих змінних, то можна знайти частинні похідні другого порядку:
сталою. Оскільки частинні похідні першого порядку для функції двох змінних є функціями цих змінних, то можна знайти частинні похідні другого порядку: 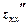 ,
, 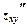 ,
, 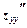 .
.
Необхідні умови екстремуму функції двох змінних
Якщо в точці 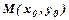 функція
функція 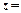
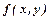 досягає екстремуму, то її частинні похідні перешого порядку в цій точці дорівнюють нулю:
досягає екстремуму, то її частинні похідні перешого порядку в цій точці дорівнюють нулю:
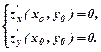
Достатні умови екстремуму функції двох змінних
Нехай в точці 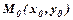 виконується умова
виконується умова 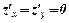 і існують частинні похідні другого порядку
і існують частинні похідні другого порядку 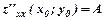 ;
; 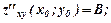
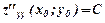 .
.
Визначимо: 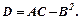
Якщо 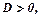 то в точці
то в точці 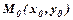 функція
функція 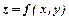 має екстремум; якщо
має екстремум; якщо 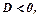 то екстремуму немає.
то екстремуму немає.
Якщо 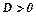 і
і 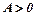 (або
(або 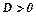 і
і 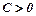 ), то функція досягає мінімуму, якщо
), то функція досягає мінімуму, якщо 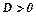 і
і 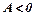 (або
(або 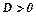 і
і 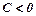 ), то функція досягає максимуму.
), то функція досягає максимуму.
Градієнтом функції двох змінних називається вектор
g = 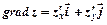 .
. 
Для функції 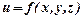 градієнт має вид
градієнт має вид
g = 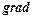
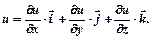
 2015-09-06
2015-09-06 269
269








