Визначений інтеграл 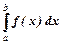 - це число, яке знаходится за формулою Ньютона-Лейбніца:
- це число, яке знаходится за формулою Ньютона-Лейбніца: 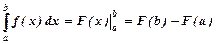 , де
, де 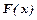 - первісна до функції
- первісна до функції 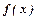 .
.
Якщо при обчиленні визначеного інтеграла 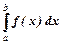 застосовують заміну змінної:
застосовують заміну змінної: 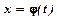 , де
, де 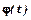 - неперервна функція, що має похідну
- неперервна функція, що має похідну 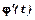 на відрізку
на відрізку 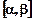 , то використовується формула
, то використовується формула
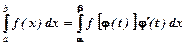 , де
, де 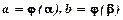 .
.
При обчисленні визначеного інтеграла не потрібно повертатись до попередньої змінної.
При методі інтегрування частинами формула має вигляд:
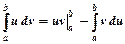 .
.
Площа 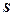 криволінійної трапеції, обмеженої кривою
криволінійної трапеції, обмеженої кривою 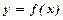 , віссю
, віссю 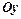 та прямими
та прямими 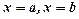 , обчислюється за формулою
, обчислюється за формулою
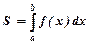
Якщо криволінійна трапеція обмежена зверху лінією 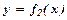 , знизу лінією
, знизу лінією 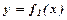 , та прямими
, та прямими 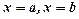 обчислюється за
обчислюється за
формулою: 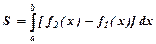 .
.
Об’єм 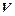 тіла обертання фігури обмеженої лініями:
тіла обертання фігури обмеженої лініями: 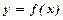 ,
, 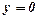 ,
, 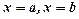 навколо осі
навколо осі 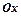 знаходимо за формулою:
знаходимо за формулою:
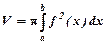 .
.
Якщо фігура, обмежена лініями: 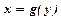 ,
, 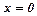 ,
, 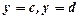 обертається навколо осі
обертається навколо осі 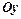 , то об’єм:
, то об’єм:
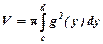
15. Невласні інтеграли.
За означенням невласні інтеграли з необмеженими межами:
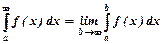 ,
, 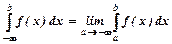 ,
,
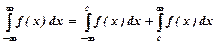 .
.
Якщо ці границі скінченні, то невласні інтеграли називаються збіжними, якщо нескінченні або не існують, то розбіжні.
Якщо підінтегральна функція 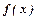 в точці
в точці 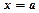 необмежена і терпить розрив, то
необмежена і терпить розрив, то 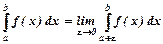 ;
;
Якщо 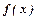 необмежена в точці
необмежена в точці 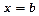 , то
, то 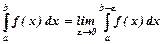 .
.
Якщо 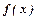 терпить розрив у внутрішній точці
терпить розрив у внутрішній точці 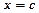 , то
, то 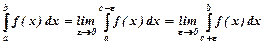 .
.
Інтеграл Пуассона: 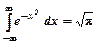 .
.
 2015-09-06
2015-09-06 753
753








