Диференціальним рівнянням першого порядку називається рівняннявигляду 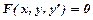 , яке, коли його можна розв’язати відносно
, яке, коли його можна розв’язати відносно 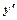 набуває вигляду
набуває вигляду 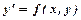 або
або 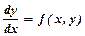 .
.
Функція 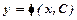 , де
, де 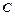 - довільна стала, називається загальним розв’язком рівняння першого порорядку, якщо при підстановці її в рівняння, вона перетворює його в правильну рівність. Якщо цей розв’язок задає функцію
- довільна стала, називається загальним розв’язком рівняння першого порорядку, якщо при підстановці її в рівняння, вона перетворює його в правильну рівність. Якщо цей розв’язок задає функцію 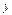 неявно:
неявно: 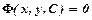 , то знайдено загальний інтеграл. При довільному
, то знайдено загальний інтеграл. При довільному 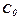 одержимо частковий розв’язок (частковий інтеграл).
одержимо частковий розв’язок (частковий інтеграл).
Задача знаходження розв’язку, який задовільняє початкові умови 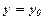 при
при 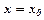 , називається задачею Коші для рівняння першого порядку.
, називається задачею Коші для рівняння першого порядку.
Розглянемо деякі класи диференціальних рівнянь, які розв’язуються в квадратурах (розв’язки виражаються через інтеграли від заданих функцій).
Диференціальне рівняння вигляду 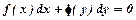 називається рівнянням з відокремленими змінними. Його загальний інтеграл:
називається рівнянням з відокремленими змінними. Його загальний інтеграл: 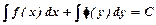 .
.
Диференціальне рівняння вигляду 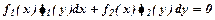 називається рівнянням з відокремлюваними змінними.
називається рівнянням з відокремлюваними змінними.
В ньому змінні можна розділити і знайти загальний інтеграл
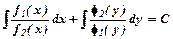 .
.
Зауваження. Часто для зручності спрощень 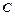 записують у вигляді
записують у вигляді 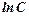 .
.
Лінійним дифрінянням першого порядку називається рівняння, яке містить шукану функцію 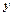 , та її похідну
, та її похідну 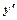 в першому степені і не містить їх добутків:
в першому степені і не містить їх добутків: 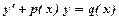 .
.
Підстановкою 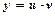 , за методом Бернулі воно приводиться до інтегрування двох дифрівнянь з відокремлюваними змінними.
, за методом Бернулі воно приводиться до інтегрування двох дифрівнянь з відокремлюваними змінними.
Однорідним дифрівнянням першого порядку називається рівняння вигляду 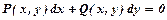 , де
, де 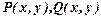 - однорідні функції одного виміру. Функція
- однорідні функції одного виміру. Функція 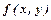 називається однорідною виміру
називається однорідною виміру 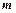 , якщо
, якщо 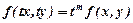 .
.
Однорідне дифрівняння зводиться до рівняння вигляду 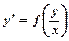 .
.
Підстановкою 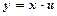 воно зводиться до рівняння з відокремлюваними змінними.
воно зводиться до рівняння з відокремлюваними змінними.
 2015-09-06
2015-09-06 455
455








