Лінійним диференціальним рівнянням другого порядку з постійними коефіцієнтами називається рівняння вигляду 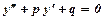 , де
, де 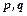 - сталі числа.
- сталі числа.
Відповідним характеристичним рівнянням називається рівняння:
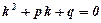 .
.
Загальний розв’язок заданого дифрівняння залежить від коренів цього характеристичного рівняння.
1. Якщо корені характеристичного рівняння дійсні та різні, 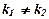 , то загальний розв’язок дифрівняння має вигляд
, то загальний розв’язок дифрівняння має вигляд 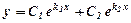 .
.
2. Якщо корені характеристичного рівняння дійсні і рівні, тобто 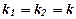 , то загальний розв’язок
, то загальний розв’язок 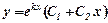 .
.
3. Якщо корені характеристичного рівняння комплексно спряжені, тобто 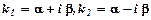 ,де
,де 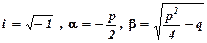 , то загальний розв’язок
, то загальний розв’язок 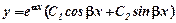 .
.
Неоднорідне лінійне дифрівняння другого порядку з постійними коефіцієнтами має вигляд 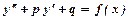 , де
, де 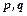 - сталі числа.
- сталі числа.
Загальний розв’язок лінійного дифрівняння (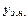 ) дорівнює сумі загального розв’язку відповідного однорідного рівняння (
) дорівнює сумі загального розв’язку відповідного однорідного рівняння (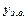 ) і довільного часткового розв’язку (
) і довільного часткового розв’язку (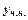 ) даного неоднорідного рівняння, тобто
) даного неоднорідного рівняння, тобто 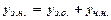
Частковий розв’язок (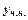 ) підбирається для деяких функцій
) підбирається для деяких функцій 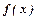 подібним до неї.
подібним до неї.
1. Нехай 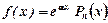 , де многочлен
, де многочлен 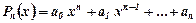 . Тоді частковий розв’язок шукаємо у вигляді
. Тоді частковий розв’язок шукаємо у вигляді
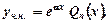 якщо
якщо 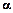 - не корінь характеристичного рівняння;
- не корінь характеристичного рівняння;
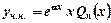 , якщо
, якщо 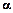 - простий корінь характеристичного рівняння;
- простий корінь характеристичного рівняння;
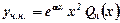 , якщо
, якщо 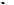
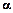 - подвійний корінь характеристичного рівняння, де
- подвійний корінь характеристичного рівняння, де 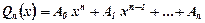 ,(
,(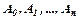 -невідомі сталі коефіцієнти, які знаходяться методом невизначених коефіцієнтів).
-невідомі сталі коефіцієнти, які знаходяться методом невизначених коефіцієнтів).
2. Нехай 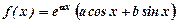 , тоді частковий розв’язок
, тоді частковий розв’язок
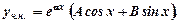 якщо
якщо 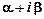 - не корінь характеристичного рівняння;
- не корінь характеристичного рівняння;
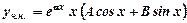 , якщо
, якщо 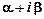 - корінь характеристичного рівняння;
- корінь характеристичного рівняння;
Для дифрівняння другого порядку загальний розв’язок містить дві довільні сталі. Задача Коші ставиться так:
Знайти такий розв’язок, який би задовільняє умови 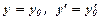 , при
, при 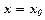 .
.
 2015-09-06
2015-09-06 308
308








