Числові ряди

Нехай задана нескінченна послідовність чисел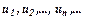

Вираз 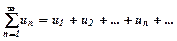називають нескінченним числовим рядом (або просто рядом), числа 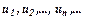– членами ряду, 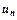– загальним членом ряду.

Частковою сумою числового ряду називають суму 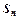перших 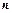членів числового ряду, тобто , ,..., .

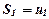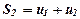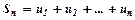Сумою 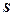числового ряду 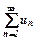називають границю його часткової суми 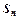при 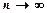, тобто .

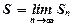Якщо границя часткової суми ряду є скінченним числом, то ряд називають збіжним і позначають .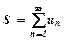

Якщо границя часткової суми ряду не існує або дорівнює 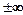, то числовий ряд називають розбіжним.

Числовий ряд вигляду 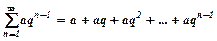називають рядом геометричної прогресії зі знаменником .

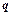При 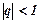ряд геометричної прогресії збігається і його сума дорівнює 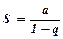. При 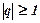ряд розбігається.

Числовий ряд вигляду 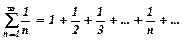називають гармонічним рядом. Цей ряд розбігається.

Необхідна ознака збіжності числового ряду.

Якщо числовий ряд 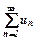збігається, то загальний член 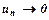при 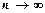, тобто .

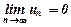Достатні ознаки збіжності числових рядів.

1. Ознака Даламбера.

Нехай усі члени числового ряду 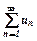додатні і при необмеженому зростанні номера 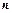, границя відношення

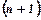-го члена до 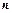-го дорівнює числу 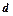. Тобто .

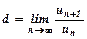Якщо 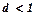, тоді числовий ряд збігається. При 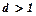, цей ряд розбігається. При 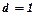потрібно застосовувати іншу ознаку.

2. Ознака порівняння. Нехай треба дослідити збіжність заданого ряду: 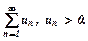Візьмемо другий додатний числовий ряд, збіжність чи розбіжність якого відома: 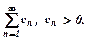Тоді:

а) якщо 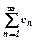ряд збігається і, починаючи з деякого номера 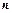, виконується співвідношення 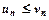, тоді й ряд 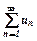також збігається.

б) якщо 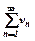ряд розбігається і, починаючи з деякого номера 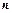, виконується співвідношення 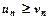, тоді й ряд 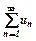також розбігається.

3. Інтегральна ознака Коші.

Нехай 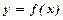-неперервна, монотонно спадна і додатна в інтервалі 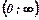функція, значення якої 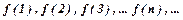дорівнюють відповідним додатним членам ряду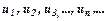

Тоді для збіжності ряду необхідно і достатньо, щоб невласний інтеграл 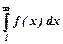мав скінченну величину.

Якщо члени числового ряду мають різні знаки, то ряд називають знакозмінним.

Ряд, члени якого почергово мають додатний та від’ємний знаки, називають знакопереміжним. Такий ряд можна записати у вигляді:

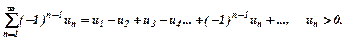Знакопереміжний ряд називають збіжним абсолютно, якщо збігається додатний числовий ряд 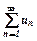, складений з абсолютних величин цього знакопереміжного ряду.

Ознака Лейбніца. Якщо абсолютні величини знакопереміжного ряду монотонно спадають 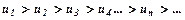і границя загального члена дорівнює нулю при 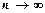, тобто виконується умова 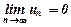, тоді знакопереміжний ряд збігається, при чому його часткова сума 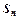обов’язково менша від першого члена ряду.

Якщо знакопереміжний ряд збігається, а ряд, складений з абсолютних величин, розбігається, то знакопереміжний ряд називають неабсолютно збіжним (або умовно збіжним).