а) метод беспосереднього інтегрування полягає в прямому застосуванні властивостей інтегралів і таблиці основних інтегралів.
б) метод заміни змінної застосовується для зведення 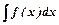 до табличного, введенням підстановки
до табличного, введенням підстановки 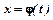 і використонням формули
і використонням формули 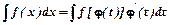 .
.
Інколи доцільно вводити заміну 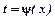 , щоб звести інтеграл до табличного.
, щоб звести інтеграл до табличного.
в) метод інтегрування частинами грунтується на використанні формули: 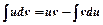 . Підінтегральний вираз подають у вигляді добутку множників
. Підінтегральний вираз подають у вигляді добутку множників 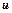 і
і 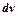 . Якщо він містить добуток многочлена на тригонометричну або показникову функцію, то за
. Якщо він містить добуток многочлена на тригонометричну або показникову функцію, то за 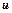 слід взяти многочлен, а все решту за
слід взяти многочлен, а все решту за 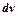 . Якщо підінтегральний вираз містить добуток многочлена на логарифмічну чи аркфункцію, то за
. Якщо підінтегральний вираз містить добуток многочлена на логарифмічну чи аркфункцію, то за 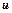 слід брати логарифмічну або аркфункцію, а решта – за
слід брати логарифмічну або аркфункцію, а решта – за 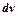 .
.
Не всякий інтеграл можна виразити через відомі елементарні функції.
Завжди інтегруються раціональні функції, які мають вигляд
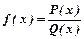 , де
, де 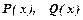 - многочлени.
- многочлени.
Якщо найвищий степінь многочлена 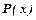 менший за найвищий степінь многочлена
менший за найвищий степінь многочлена 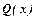 , то дріб називають правильним, в іншому випадку неправильним.
, то дріб називають правильним, в іншому випадку неправильним.
З неправильного дробу виділяють цілу частину шляхом ділення двох многочленів і, таким чином, зводять інтегрування його до інтегрування цілої раціональної функції і правильного дробу.
Правильний дріб можна розкласти на суму найпростіших дробів чотирьох типів:
1) 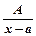 ; 2)
; 2) 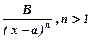 ; 3)
; 3) 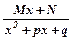 ; 4)
; 4) 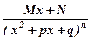 , кожен з яких інтегрується.
, кожен з яких інтегрується.
Інтеграли виду 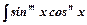 , якщо
, якщо 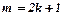 непарне число, обчислюється підстановкою
непарне число, обчислюється підстановкою 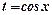 , якщо
, якщо 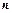 непарне число – підстановкою
непарне число – підстановкою 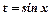 . Якщо обидва показники парні, то використовуючи формули пониження степеня тригонометричних функцій:
. Якщо обидва показники парні, то використовуючи формули пониження степеня тригонометричних функцій:
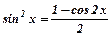 ,
, 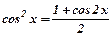 ,
, 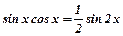 , прийдемо до обчислення інтегралів, в яких хоч один із степенів буде непарним.
, прийдемо до обчислення інтегралів, в яких хоч один із степенів буде непарним.
Інтеграли типу 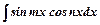 ,
, 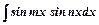 ,
,
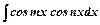 перетворюють з використанням формул перетворення добутку тригонометричних функцій у суму.
перетворюють з використанням формул перетворення добутку тригонометричних функцій у суму.
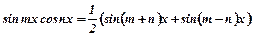 ,
,
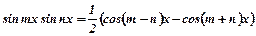 ,
,
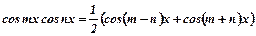 .
.
Інтеграли типу 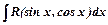 , де
, де 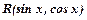 - раціональна функція від
- раціональна функція від 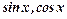 можна звести до інтегрування раціональних дробів за допомогою універсальної підстановки
можна звести до інтегрування раціональних дробів за допомогою універсальної підстановки 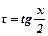 , скориставшись формулами
, скориставшись формулами 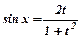 ,
, 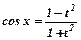 ,
, 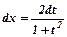 .
.
Інтеграли від ірраціональних функцій
1) 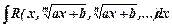 , де підінтегральна функція раціональна відносно
, де підінтегральна функція раціональна відносно 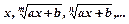 зводять до інтегралів від раціональних функцій підстановкою
зводять до інтегралів від раціональних функцій підстановкою 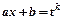 , де
, де 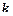 - найменше спільне кратне чисел
- найменше спільне кратне чисел 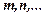
2) Для 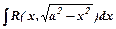 використовують підстановку
використовують підстановку
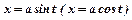 ; для
; для 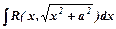 -
- 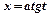 (
(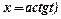 .
.
 2015-09-06
2015-09-06 704
704








