Рассмотрим следующее гиперболическое уравнение, записанное в цилиндрической системе координат:
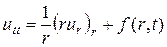 (2.15)
(2.15)
При построении разностной схемы будем использовать следующий шаблон (рис.6):
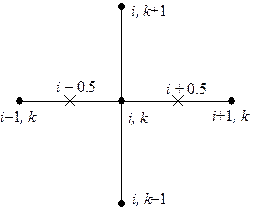
Рис.6.
Производная по времени записывается также как и п.2.1, а производная по пространству: 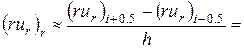
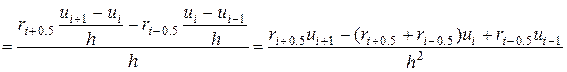 .
.
Здесь 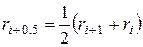 .
.
Тогда разностная схема для уравнения (2.15) будет иметь вид:
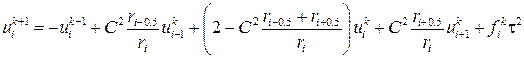 ,
,
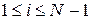
На первом шаге по времени: (k =0)
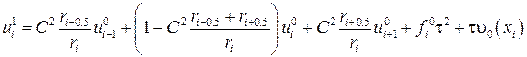
Граничные условия реализуются по аналогии с п.2.2, за исключением того случая, когда левая граница есть центр симметрии, т.е. 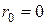 . На такой границе должно быть задано условие симметрии:
. На такой границе должно быть задано условие симметрии: 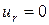 . Для нахождения решения на верхнем временном слое в узле i = 0, уравнение (1.11) нельзя применять, как это делалось в п.1.2 с уравнением (1.2), поскольку в данном случае существует особенность при
. Для нахождения решения на верхнем временном слое в узле i = 0, уравнение (1.11) нельзя применять, как это делалось в п.1.2 с уравнением (1.2), поскольку в данном случае существует особенность при 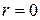 .
.
Для устранения этой особенности перепишем уравнение (1.10) в виде 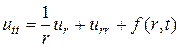 . Устремляя
. Устремляя 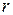 к нулю и раскрывая по Лопиталю неопределенность
к нулю и раскрывая по Лопиталю неопределенность 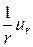 , получим следующее уравнение в точке
, получим следующее уравнение в точке 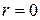 :
:
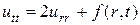 (2.16)
(2.16)
Записывая разностную схему для (2.16) и для граничного условия 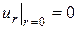 , получим следующее уравнения для нахождения функции на верхнем временном слое в узле i = 0:
, получим следующее уравнения для нахождения функции на верхнем временном слое в узле i = 0:
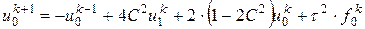 ,
, 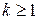 (2.17)
(2.17)
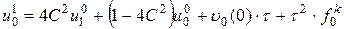 ,
, 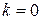
Условие устойчивости 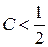
Для краевых условий 2-го рода:
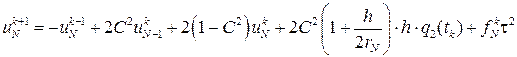 , k > 0
, k > 0
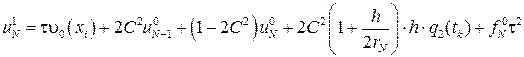 , k = 0
, k = 0
 2015-09-06
2015-09-06 377
377








