Общая формула математического решения задачи обмена двух товаров друг на друга
92. (…)
…Предположим, что держатель (1) товара (В), потребности которого в (А) и (В) все также выражаются двумя уравнениями r = φa,1(q), r = φb,1(q) кривых потребностей αr,1αq,1βr,1βq,1, вместо того, чтобы прийти на рынок с нулевым количеством (А) и с количеством q b (В), представленным Oq b (рис. 3), является на него с количеством q q,1 (А), представленном Oq a,1 (рис. 4) и количеством q b,1 (В), представленным Oq b,1; a теперь попробуем выразить его спрос на (В) в зависимости от цены p b и его спрос на (А) в зависимости от цены р a.
Если при цене p b товара (В) в (А), представленной длиной q b,1 p b, он спрашивает количество d b (В), представленное длиной q b,1 d b, то он должен будет предложить количество o a (А), представленное длиной q a,1 o a, причем такое, чтобы величины р b, d b и о a были связаны уравнением
o a = d b p b
Так как интенсивность его последней удовлетворенной потребности в (В) есть r b, представленная длиной d bβ, а интенсивность его последней удовлетворенной потребности в (А) есть r a, представленная длиной о aα, то по теореме максимального удовлетворения мы получим (§80)
r b = p b r a.
или, заменяя r b и r a, на их значения,
[4] φb,1(q b,1 + d b) = p bφa,1(qa,1– o a) = p bφa,1(qa,1– d b p b),
уравнение кривой b d,1 b p,1 спроса на (В) как функции от цены (В) в товаре (А), построенной в осях q b,1 q, q b,1 p.
Равным образом, если при цене р a товара (А) в (В) наш человек спрашивает количество d a (А), то он должен будет предложить количество о b (В), причем такое, чтобы величины р a, d a и о b были связаны уравнением
o b = d a p a.
Так как интенсивность его последней удовлетворенной потребности в (А) есть r a, а интенсивность его последней удовлетворенной потреб-1 ности в (В) есть r b, то мы получим
r a = p a r b
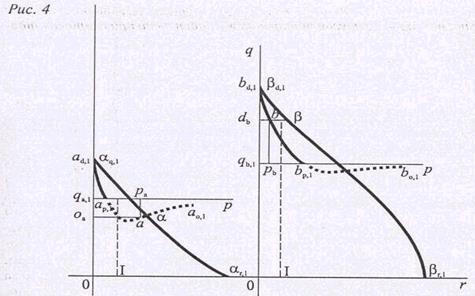
или
[5] φa,1(q a,1 + d a) = p aφb,1(qb,1– o b) = p aφb,1(qb,1– d a p a),
уравнение кривой αd,1 αp,1 спроса на (А) как функции от цены (А) в товаре (В), постороенной в осях q a,1 q, q a,1 p.
93. Обсуждение двух уравнений [4] и [5] для разных случаев – спроса по нулевой цене, цены при нулевом спросе, предложения, равного \ наличному количеству, уменьшения или увеличения наличных количеств – будет совершенно аналогичным приведенному выше. Поэтому я не буду этого делать, за исключением особого пункта, который важно отметить.
Если в уравнении [4] принять db = 0, то оно становится
φb,1(q b,1 + d a) = p bφb,1(qb,1)
Поскольку мы имеем, как и раньше, отношение p a p b = 1, то данное уравнение может быть выражено в форме
φa,1(q a,1) = p aφb,1(qb,1).
Мы могли бы также получить его, принимая в уравнении [5] d a = 0.
Таким образом: если спрос на один из двух товаров при некоторой цене равен нулю, то спрос на другой товар также равен нулю при соответствующей цене.
94. Но данная теорема соответствует более общей теореме.
Чтобы преобразовать уравнение [4] спроса на (В) как функцию от цены (В) в (А) в уравнение предложения (А) как функцию от цены (А) в (В), достаточно заменить в нем d bна o a p a на 1/ p a. Тем самым оно станет
φa,1(q a,1 – o a) = p aφb,1(qb,1 + o a p a),
уравнение, являющееся не чем иным, как уравнением [5], в котором d a заменено на (– o a). Таким образом, уравнение [5] спроса на (А) есть уравнение предложения (А) при отрицательных значениях d a. Равным образом можно доказать, что уравнение [4] спроса на (В) есть уравнение предложения (В) при отрицательных значениях d b. Однако, поскольку цены, по существу, положительны, то когда d b положительно, то o a = d b p b положительно и, следовательно, d a = – o a отрицательно; а когда db отрицательно, то o a = d b p b отрицательно и, следовательно, d a = – o a положительно. Равным образом можно было бы доказать, что когда с/а положительно, то d b отрицательно, а когда d a отрицательно, d b положительно.
Итак: если спрос на один из двух товаров при некоторой цене положителен, то при соответствующей цене спрос на другой товар отрицателен, или его предложение положительно.
Действительно, держатель обоих товаров может предъявлять спрос на один из них лишь при условии, что он предлагает другой (товар), и обратно. Отсюда следует, что если он не спрашивает и не предлагает никакого количества одного из них, то он не предлагает и не запрашивает никакого количества другого (товара). Это, как нетрудно признать, тот случай, когда – при равенстве соотношения редкостей двух товаров точно цене одного из них в другом – имеет место максимум действительной полезности.
95. Кривые являются, таким образом, кривыми спроса от точки αd,1, до точки αp,1 и от точки bd,1 до точки bр,1, а точки αp,1, bp,1 являются взаимосвязанными (обратными). А в части, обозначенной на рисунке пунктиром и лежащей ниже осей q a,1 p, q b,1 p, кривые являются кривыми предложения отточки αp,1 до точки αo,1 и от b o,1. Взятые в целом относительно оси Or, каждая из них является кривой совокупного количества – сохраненного у себя и полученного – каждого из двух товаров в зависимости от цены. Она имеет минимум, соответствующий максимальному предложению в обмен другого товара.
96. Коротко говоря, если мы просто обозначим через х 1 и у 1, количества, положительные либо отрицательные, товара (А) и (В), которые обменивающееся лицо (1) будет в зависимости от цены добавлять к количествам q a,1, q b,1 этих товаров, держателем которых он является, то намерения к торгу данного индивида будут вытекать из двух уравнений обмена и максимального удовлетворения
x 1 v a + y 1 v b = 0
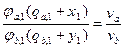
в которых можно исключить y 1, чтобы получить x 1, как функцию от p а, или исключить x 1, чтобы получить y 1 как функцию от pb. Полученные таким путем формулы
φa,1(q a,1 + x 1) = p aφb,1(qb,1 – x 1 p a),
φb,1(q b,1 + y 1) = p bφa,1(qa,1 – y 1 p b),
являются общими формулами, которые могут быть должным образом развернуты, чтобы выразить намерения к торгу того же самого индивида в случае обмена нескольких товаров друг на друга.
Существенно важно отметить, что первое из этих уравнений – для значений pa, делающих отрицательный x1 больше q a,1, должно быть заменено уравнением х 1 = – q a,1, в этом случаев; будет задано уравнением y1p b= q a,1; равным образом второе уравнение – для значений р b, делающих отрицательный y 1 больше q b,1, – должно быть заменено уравнением y 1 = – q b,1, в этом случае x 1 будет задано уравнением х 1 p a = q b,1.
97. Эти-уравнения, решенные относительно x 1 и у 1, и расположенные должным образом, чтобы удовлетворить предшествующему ограничению, примут форму:
x 1 = f a,1(p a), y 1 = f b,1(p b).
Таким же образом, чтобы выразить намерения к торгу обменивающихся лиц (2), (3).... мы будем иметь
x 2 = f a,2(p a), y 2 = f b,2(p b),
x 3 = f a,3(p a), y 3 = f b,3(p b)ю
А равенство, действительных предложения и спроса по каждому из двух товаров (А) и (В)будет выражаться уравнениями:
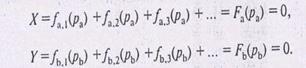
p a можно, например, получить из первого уравнения, тогда р b будет определено из уравнения
p a p b = 1;
и это значение р b будет с необходимостью удовлетворять второму уравнению в силу того, что мы имеем, естественно,
Xv a +Yv b = 0,
откуда следует, что, если Fa (p a) = 0 при определенном значении р a, то F (p b) = 0 при соответствующем значении р и.
Это решение является аналитическим. Ему можно придать геометрический вид. Сумма положительных х даст кривую спроса на (А), а сумма положительных у даст кривую спроса на (В). Из этих двух кривых спроса выводятся обе кривые предложения двух товаров, которые являются, впрочем, не чем иным, как суммами отрицательных х и у, взятых с положительным знаком. Пересечение кривых определяет текущие цены.
98. Таким будет математическое решение. А решение на рынке будет происходить следующим образом.
После того, как «выкрикнуты» две какие-либо взаимосвязанные цены pa и p b, то x 1, x 2, x 3… y 1, y 2, y 3… будут определяться без каких-либо расчетов, но тем не менее в соответствии с условием максимального удовлетворения. Тем самым будут определены Х и Y. Если мы будем иметь Х = 0, то У также будет равен 0, а цены будут равновесными. Но обычно мы будем иметь Х ≷ 0 и, следовательно, Y ≷ 0. Первое неравенство может быть выражено в форме
D a ≷ O a
если обозначить через D a сумму положительных х и через О a сумму отрицательных х, взятых с положительным знаком. Речь идет о том, чтобы сделать D a равным О a.
Что касается D a, то это количество положительно при р a = 0; оно стремится к нулю, если р a растет; оно равно нулю при определенном значении p a, заключенном между нулем и бесконечностью. Что касается О aто это количество равно нулю при p a = 0 и даже при некоторых положительных значениях p a; затем оно растет, если растет p a, но не бесконечно: оно проходит, по меньшей мере, через один максимум, затем уменьшается, если р a продолжает расти; и оно равно нулю при p a = ∞. В этих условиях – если только D a не становится равным нулю до того, как О a перестало быть нулевым, случай, при котором нет решения –существует некоторое значение p a, при котором О a и D a равны. Чтобы найти это значение, надо увеличивать p a, если D a > О a и уменьшать p a, если D a < Оa. Мы узнаём здесь закон действительных предложения и спроса.
 2015-09-06
2015-09-06 433
433








