В случае дискретного спектра энергии частицы нас, как и прежде, будет интересовать среднее число частиц 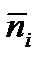 в заданном i -ом квантовом состоянии с энергией
в заданном i -ом квантовом состоянии с энергией 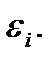 Зависимость величины
Зависимость величины 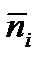 от энергии
от энергии 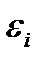 определяет распределение по состояниям частиц квантового идеального газа с дискретным спектром энергии. В квантовой статистической физике показывается, что эта зависимость имеет вид
определяет распределение по состояниям частиц квантового идеального газа с дискретным спектром энергии. В квантовой статистической физике показывается, что эта зависимость имеет вид
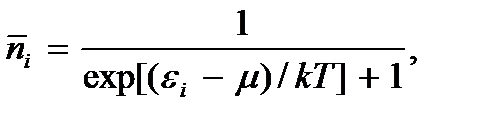 (3.22)
(3.22)
где μ – уже упоминаемый выше химический потенциал частицы. Функция (3.22) называется функцией распределения Ферми- Дирака частиц по энергиям в случае дискретного спектра. Так как в случае фермионов каждое состояние может быть либо занято, либо свободно, – в среднем занято не больше, чем один раз (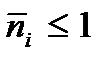 ). Поскольку экспонента – величина положительная, то из (3.22) следует, что
). Поскольку экспонента – величина положительная, то из (3.22) следует, что 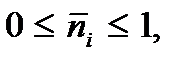 так что распределение Ферми – Дирака удовлетворяет принципу Паули: в каждом квантовом состоянии может находиться не более одного фермиона с определенным направлением спина.
так что распределение Ферми – Дирака удовлетворяет принципу Паули: в каждом квантовом состоянии может находиться не более одного фермиона с определенным направлением спина.
Заметим, что величина 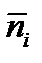 изменяется в тех же пределах
изменяется в тех же пределах 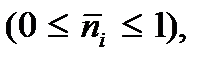 что и вероятность, поэтому функцию (3.22) можно рассматривать как вероятность
что и вероятность, поэтому функцию (3.22) можно рассматривать как вероятность 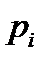 заполнения уровня энергии
заполнения уровня энергии 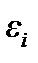 .
.
При абсолютном нуле температуры распределение Ферми – Дирака имеет вид
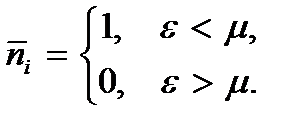
Действительно, при 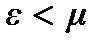 показатель степени экспоненты стремится к
показатель степени экспоненты стремится к  а сама экспонента – к нулю; при
а сама экспонента – к нулю; при 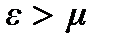 показатель степени экспоненты и сама экспонента стремятся к
показатель степени экспоненты и сама экспонента стремятся к 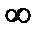 , а функция
, а функция 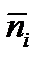 – нулю. График такого распределения показан на рис. 3.6. На рис. 3.6 видно, что при абсолютном нуле температуры все уровни вплоть до уровня с энергией
– нулю. График такого распределения показан на рис. 3.6. На рис. 3.6 видно, что при абсолютном нуле температуры все уровни вплоть до уровня с энергией 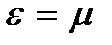 заняты электронами, а все вышележащие уровни свободны. Последний заполненный уровень энергии при абсолютном нуле температуры называется уровнем (или энергией) Ферми (обозначают
заняты электронами, а все вышележащие уровни свободны. Последний заполненный уровень энергии при абсолютном нуле температуры называется уровнем (или энергией) Ферми (обозначают 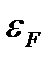 ). Следовательно, химический потенциал μ фермионов – это энергия Ферми. При температуре
). Следовательно, химический потенциал μ фермионов – это энергия Ферми. При температуре 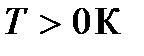 химический потенциал – это уровень энергии, средняя заполненность которого равна одной второй:
химический потенциал – это уровень энергии, средняя заполненность которого равна одной второй: 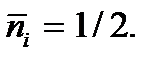 Можно сказать также, что уровень Ферми – это уровень, вероятность заполнения которого равна
Можно сказать также, что уровень Ферми – это уровень, вероятность заполнения которого равна 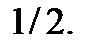
В случае бозонов среднее число частиц в квантовом состоянии с энергией 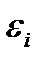 определяется как
определяется как
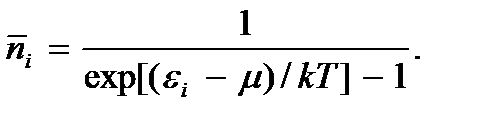 (3.23)
(3.23)
Эта функция называется распределением Бозе – Эйнштейна по энергии частиц в случае дискретного спектра.
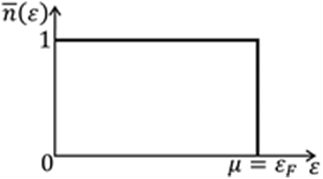 Рис. 3.6 Рис. 3.6 |
Как видим, распределение Бозе – Эйнштейна отличается от распределения Ферми – Дирака только знаком перед единицей в знаменателе. Видим также, что величина 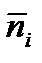 может принимать любые значения. Так и должно быть. Поскольку бозоны принципу Паули не подчиняются и число их в каждом состоянии не ограничено. Химический потенциал бозонов
может принимать любые значения. Так и должно быть. Поскольку бозоны принципу Паули не подчиняются и число их в каждом состоянии не ограничено. Химический потенциал бозонов 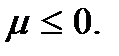
Если 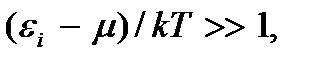 то единицей в формулах (3.22) и (3.23) можно пренебречь; различия между распределениями Ферми – Дирака и Бозе – Эйнштейна исчезают, и оба распределения переходят в распределение Больцмана (3.8). При этом
то единицей в формулах (3.22) и (3.23) можно пренебречь; различия между распределениями Ферми – Дирака и Бозе – Эйнштейна исчезают, и оба распределения переходят в распределение Больцмана (3.8). При этом 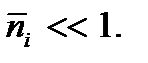 Указанное выше условие выполняется при высоких температурах.
Указанное выше условие выполняется при высоких температурах.
В случае непрерывного спектра энергии, как и прежде, можно пользоваться квазиклассическим приближением. Наличие спина учитывается тем, что в число параметров состояния частицы включается спиновое магнитное квантовое число 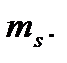 Теперь вместо среднего числа частиц на i -ом энергетическом уровне вводится среднее число частиц
Теперь вместо среднего числа частиц на i -ом энергетическом уровне вводится среднее число частиц 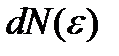 с энергией, заключенной в интервале от
с энергией, заключенной в интервале от 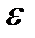 до
до 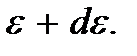 Имеем
Имеем 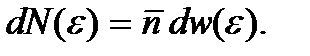 Величина
Величина 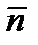 определяется в виде (3.18) или (3.20), в которых вместо
определяется в виде (3.18) или (3.20), в которых вместо 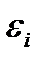 теперь следует писать
теперь следует писать 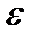 – значение энергии из интервала от
– значение энергии из интервала от 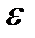 до
до 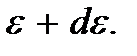 Число состояний
Число состояний 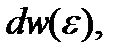 отвечающих данному энергетическому интервалу, определяется выражением (3.4). Наличие спина у частицы приводит к увеличению числа состояний в
отвечающих данному энергетическому интервалу, определяется выражением (3.4). Наличие спина у частицы приводит к увеличению числа состояний в 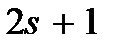 раз, так как при одной и той же энергии частицы возможно
раз, так как при одной и той же энергии частицы возможно 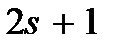 ориентации ее спина. Поэтому в правой части выражения (3.4) следует поставить множитель
ориентации ее спина. Поэтому в правой части выражения (3.4) следует поставить множитель 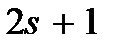 . С учетом этого будем иметь
. С учетом этого будем иметь
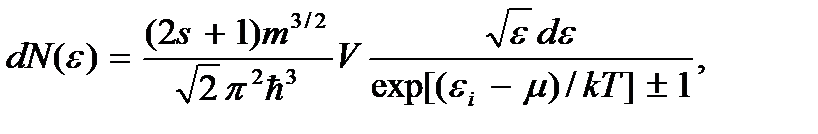 (3.24)
(3.24)
где знак плюс соответствует распределению Ферми – Дирака, а минус – распределению Бозе – Эйнштейна.
При 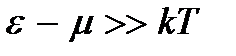 и
и 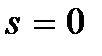 соотношение (3.25) принимает вид.
соотношение (3.25) принимает вид.
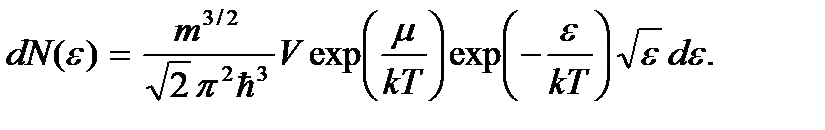
Сравнивая это выражение с выражением (3.14), видим, что оно переходит в формулу распределения Максвелла – Больцмана по кинетической энергии, если положить
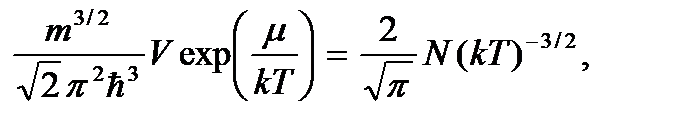
откуда получаем выражение химического потенциала
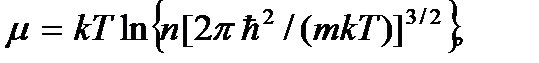
где 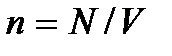 – концентрация газа. Условие
– концентрация газа. Условие 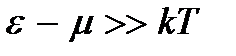 можно заменить условием
можно заменить условием  из которого следует условие
из которого следует условие
 (3.25)
(3.25)
Мы пришли к критерию применимости классической статистики Максвелла к идеальному газу. Как видим, оно выполняется тем точнее, чем меньше концентрация газа и чем выше его температура. При выполнении обратного неравенства идеальный газ меняет свои свойства; он становится вырожденным, и его следует описывать с помощью квантовых статистик.
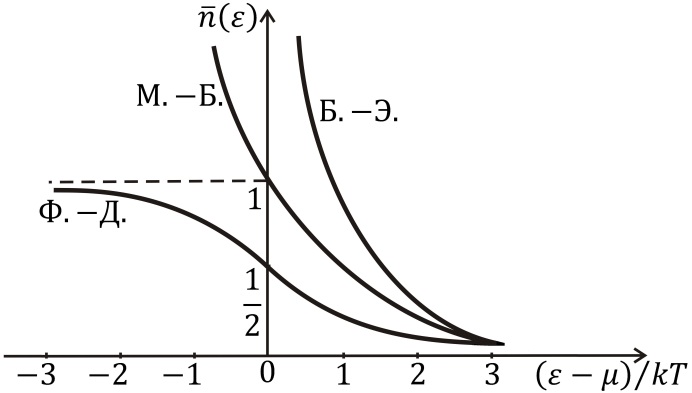
Рис. 3.7
Опыт показывает, что обычные молекулярные газы в широком интервале концентраций и температур удовлетворяют условию (3.25) и, следовательно, допускают классическое или квазиклассическое описание.
Распределения Ферми – Дирака и Бозе – Эйнштейна в случае непрерывного спектра изображены на рис. 3.7. Здесь же показано и распре-
деление Максвелла – Больцмана. При больших значениях аргумента 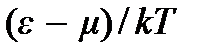 , когда среднее число частиц, приходящихся на каждое со- стояние с энергией
, когда среднее число частиц, приходящихся на каждое со- стояние с энергией 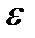 , оказывается много меньше единицы, оба квантовых распределения переходят в классическое распределение Максвелла – Больцмана
, оказывается много меньше единицы, оба квантовых распределения переходят в классическое распределение Максвелла – Больцмана
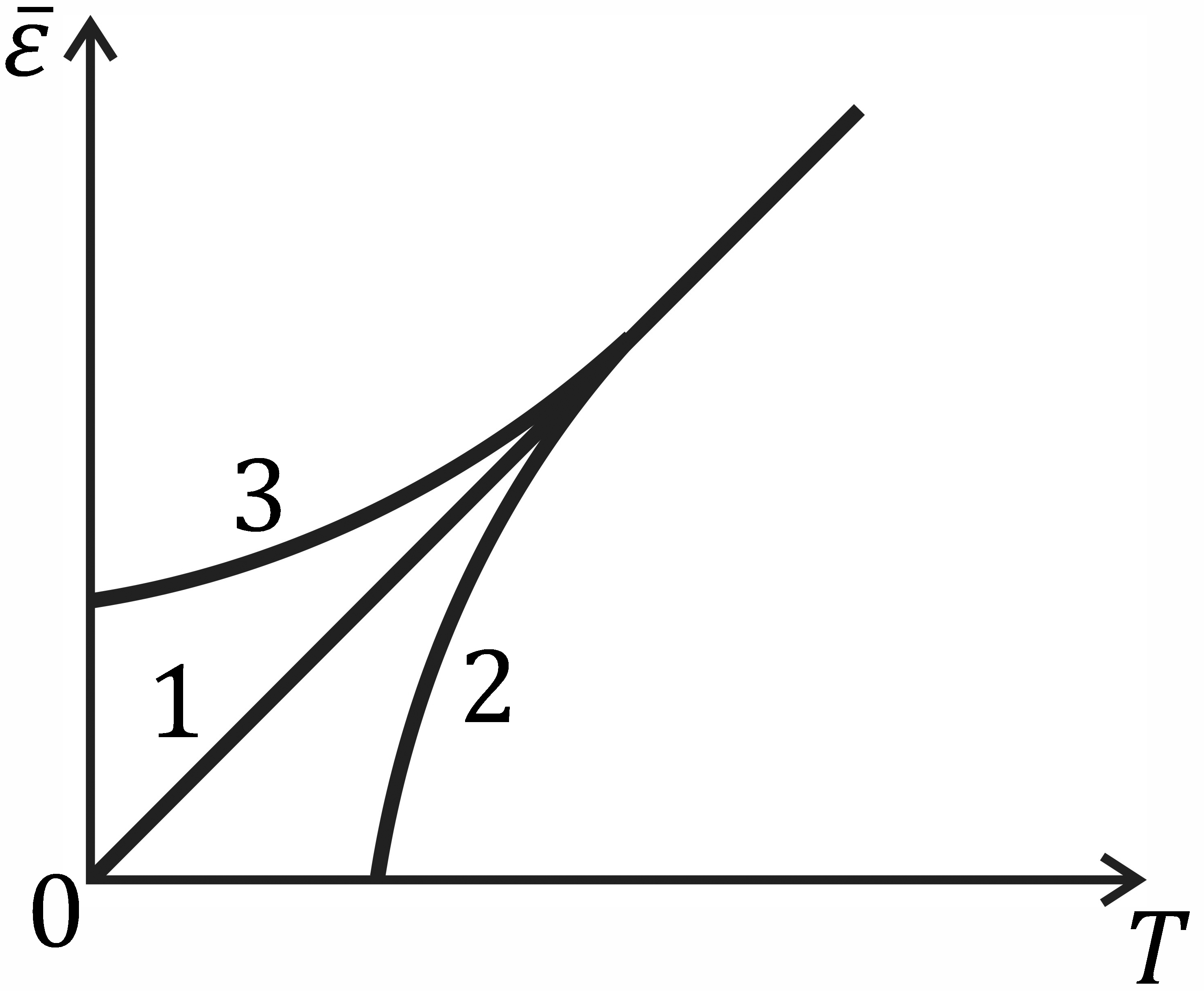
Рис. 3.8
На рис. 3.8 приведены зависимости от температуры средней кинетической энергии поступательного движения частиц – классического газа (1), бозе-газа (2) и ферми-газа (3). Как видим, в области вырождения, т.е. в области состояний, в которых проявляются квантовые свойства газа, и, следовательно, возникают отступления его от распределения Максвелла – Больцмана, средняя энергия поступательного движения частиц не является линейной функцией температуры (кривые 2 и 3). При этом поступательное движение бозе-частиц прекращается раньше, чем температура принимает значение абсолютного нуля. Наоборот, ферми-частицы сохраняют некоторую энергию и при абсолютном нуле, называемую нулевой энергией. В области вырождения определение температуры как меры средней энергии поступательного движения молекул газа уже не верно. При высоких температурах все три кривые сливаются в одну – все распределения переходят в распределение Максвелла – Больцмана.
 2015-09-06
2015-09-06 6337
6337
