Получение двухмерного дискретного аналога

Сначала найдем аппроксимацию двухмерного уравнения, затем ту же процедуру применим и к трехмерному случаю. Рассмотрим контрольный объем (рис. 5.8). Используя опыт, приобретенный при анализе одномерной задачи для получения суммарного теплового потока J_e, и предположив, что найденное выражение применимо ко всей грани КО площадью Dy*1, сможем сразу записать дискретный аналог для двухмерной задачи.

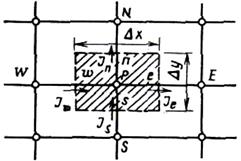Рис 5.8 КО (заштрихованная область) для двухмерного случая

При рассмотрении одномерного случая было, показано, что aP=aE+aW только тогда, когда удовлетворено уравнение неразрывности. Таким образом, правило относительно суммы соседних коэффициентов (правило 4) может быть удовлетворено только тогда, когда в рассмотрение включено уравнение неразрывности. Уравнение (5.12) в двухмерной форме можно представить в виде ,

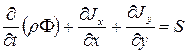где J_x и J_y - суммарные (конвекция плюс диффузия) потоки, определенные следующим образом:

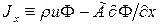и ,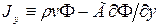

где u, v - компоненты скорости в направлениях осей x и y.

Когда заданные поля скорости и плотности удовлетворяют дискретному аналогу уравнения неразрывности – проблем нет. Однако когда заданные поля не удовлетворяют уравнению неразрывности, то разные способы записи приводят к разным решениям.

В каком случае можно встретиться с полями течения, которые не удовлетворяют уравнению неразрывности? Такая возможность появляется, поскольку часто поле течения не является действительно заданным, а рассчитывается итерационным методом точно так же, как и зависящий от T коэффициент теплопроводности в задаче теплопроводности.

Перед тем как достигается окончательная сходимость, приближенные поля течения на промежуточных итерациях могут не удовлетворять уравнению неразрывности. По этой причине необходимо специально заботиться о соблюдении правила 4.

Двухмерный дискретный аналог можно записать в следующем виде

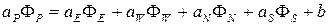, (5.13)

где , ,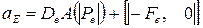

, ,

,

, .

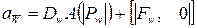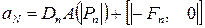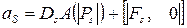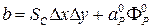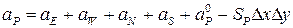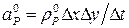Здесь Ф _P⁰ н r_P⁰ обозначают известные значения для времени t, а все другие величины (Ф _P, Ф _E, Ф _W, Ф _N, Ф _S и т.д.) представляют собой неизвестные величины для времени t+Dt. Массовые расходы F_e, F_w, F_n, и F_s определены уравнениями

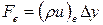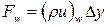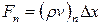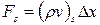, , , (5.14)

Соответствующие проводимости представим в виде

, ,

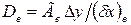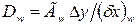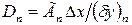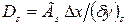, (5.15)

а числа Пекле

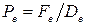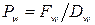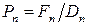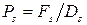, , , (5.16)

Функцию A( | P |) можно взять из таблицы 5.1 соответственно выбранной схеме.

Следует отметить, что даже на этой стадии физический смысл различных коэффициентов в (5.13) понятен. Коэффициенты в соседних точках a_E, a_W, a_N и a_S учитывают влияние конвекции и диффузии для четырех граней КО, которые зависят от массового расхода F и проводимости D. Член a_P⁰ Ф _P⁰ характеризует известную величину Ф для КО (для времени t), отнесенную к шагу по времени. Оставшиеся члены, можно интерпретировать аналогичным образом.