Енергія Гіббса

Енергією Гіббса називають функцію стану, що визначають у такий спосіб:

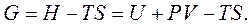. (4.20)

Її повний диференціал дорівнює:

^.

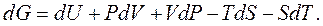Оскільки 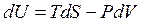, то .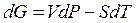

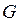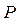Отже, природними змінними для функції є і 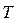, а часткові похідні цієї функції:

(4.21)

Якщо температура та тиск залишаються постійними, співвідношення (4.13) можна записати у вигляді:

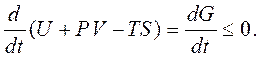
(4.22)

Звідси випливає, що необоротний процес за сталих тиску та температури супроводжується зменшенням енергії Гіббса. У стані рівноваги системи енергія Гіббса мінімальна.