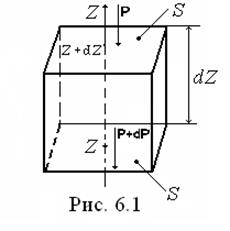
Розглянемо закон розподілу мікрочастинок за потенціальними енергіями на прикладі молекул ідеального газу, що перебуває в полі тяжіння. Нехай сили поля спрямовані уздовж осі 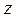 (рис. 6.1). Очевидно, що тиск газу в різних точках уздовж осі буде різним. Виберемо дві площини
(рис. 6.1). Очевидно, що тиск газу в різних точках уздовж осі буде різним. Виберемо дві площини 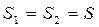 , орієнтовані перпендикулярно осі z і які розташовані одна від одної на відстані
, орієнтовані перпендикулярно осі z і які розташовані одна від одної на відстані 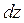 . Якщо тиски газу на обох площинах рівні Р і
. Якщо тиски газу на обох площинах рівні Р і 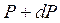 , то різниця тисків
, то різниця тисків 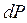 повинна дорівнювати сумарній силі, що діє на частинки газу, вміщені в об'ємі паралелепіпеда з основою
повинна дорівнювати сумарній силі, що діє на частинки газу, вміщені в об'ємі паралелепіпеда з основою 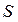 і висотою
і висотою 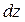 , віднесеній до площі основи:
, віднесеній до площі основи:
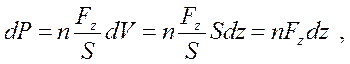 |
де 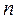 – концентрація молекул газу в цьому об'ємі, а
– концентрація молекул газу в цьому об'ємі, а 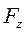 – сила, що діє на одну молекулу газу в точці з координатою
– сила, що діє на одну молекулу газу в точці з координатою  .
.
Сила 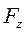 пов'язана з потенціальною енергією
пов'язана з потенціальною енергією 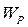 молекули співвідношенням
молекули співвідношенням 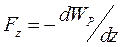 . Таким чином, додатковий тиск
. Таким чином, додатковий тиск 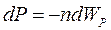 .
.
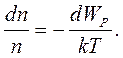 Вважаючи температуру розглянутого ідеального газу у всіх точках однаковою, на підставі рівняння Мендєлєєва–Клапейрона знаходимо, що
Вважаючи температуру розглянутого ідеального газу у всіх точках однаковою, на підставі рівняння Мендєлєєва–Клапейрона знаходимо, що 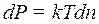 . Співставляючи два останні рівняння для
. Співставляючи два останні рівняння для 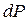 , отримаємо:
, отримаємо:
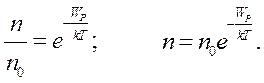 Інтегрування цього виразу з наступним потенціюванням дасть такий результат:
Інтегрування цього виразу з наступним потенціюванням дасть такий результат:
|
Тут 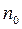 та
та 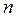 – концентрації молекул газу в станах з умовно прийнятою нульовою потенціальною енергією й потенціальною енергією
– концентрації молекул газу в станах з умовно прийнятою нульовою потенціальною енергією й потенціальною енергією 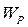 відповідно.
відповідно.
Рівняння (6.5) називають законом розподілу Больцмана. Це рівняння може бути отримане шляхом більш загальних теоретичних міркувань і має універсальний характер. Воно може бути застосовано до будь-яких систем мікрочастинок, які розташовані в різних потенціальних полях.
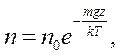 Стосовно до поля тяжіння Землі на невеликій висоті рівняння (6.5) набирає вигляду:
Стосовно до поля тяжіння Землі на невеликій висоті рівняння (6.5) набирає вигляду:
(6.6)
де 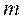 – маса молекули.
– маса молекули.
Для двох різних станів з потенціальними енергіями 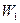 та
та 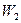 одержимо:
одержимо:
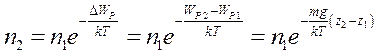 |
(6.7)
Оскільки тиск газу 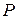 зв'язаний з його концентрацією
зв'язаний з його концентрацією 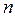 співвідношенням
співвідношенням 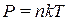 , то на підставі рівнянь (6.6) знаходимо:
, то на підставі рівнянь (6.6) знаходимо:
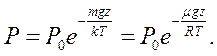 (6.8)
(6.8)
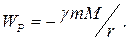
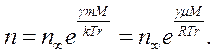 Тут
Тут 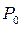 і
і 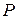 тиски газу на поверхні Землі та на висоті
тиски газу на поверхні Землі та на висоті 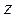 відповідно,
відповідно, 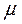 – молярна маса газу. Рівняння (6.8) називають барометричною формулою. У випадку значних висот потенціальну енергію потрібно прийняти рівною
– молярна маса газу. Рівняння (6.8) називають барометричною формулою. У випадку значних висот потенціальну енергію потрібно прийняти рівною
Тоді рівняння (6.6) і (6.8) набирають вигляду:
(6.9)
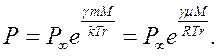 |
(6.10)
Тут 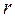 – відстань від центра Землі до даної точки простору,
– відстань від центра Землі до даної точки простору, 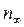 та
та 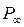 – концентрація молекул і тиск газу на нескінченно великих відстанях від Землі.
– концентрація молекул і тиск газу на нескінченно великих відстанях від Землі.
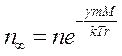 З рівняння (6.10) випливає, що концентрація молекул газу на нескінченно великій висоті над Землею:
З рівняння (6.10) випливає, що концентрація молекул газу на нескінченно великій висоті над Землею:
(6.11)
відмінна від нуля. Це суперечить досвіду, оскільки земна атмосфера не перебуває в стані теплової рівноваги. Закон розподілу Больцмана знаходить дослідне підтвердження. Як приклад радимо студентам самостійно розглянути досліди Перрена з визначення числа Авогадро за [1], [2], [3].
 2015-09-06
2015-09-06 889
889








