Иерархическая таксономия

Можно считать, что исходное множество 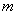точек представляет собой результат таксономии с радиусом 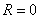, при котором получается 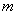таксонов, каждый из которых содержит по одной точке. Применим к ним алгоритм BIGFOR, исключив из него описанную выше процедуру перераспределения точек. На первом шаге алгоритма BIGFOR выбирается небольшой радиус 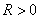, дающий 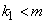таксонов первого уровня. На втором шаге происходит слияние некоторых близких друг к другу мелких таксонов в более крупные, в результате чего появляются 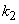таксонов второго уровня 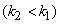. Если эти шаги продолжать, то на некотором шаге 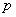будет получена таксономия, объединяющая все точки в один-единственный таксон.

Отношения между таксонами разных уровней можно представить себе в виде иерархической структуры или дерева, состоящего из 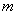объектов на нулевом уровне (уровне листьев) и 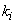таксонов 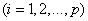на каждом из 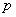уровней. Корневая 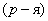вершина этого дерева содержит 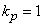таксон со всеми 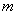объектами. Из нее выходит 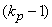ребер, соединяющих корневую вершину с центрами таксонов 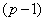-го уровня. Такие связи между таксонами прослеживаются вплоть до 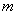ребер, которые соединяют 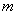точек нулевого уровня с 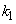центрами самых мелких таксонов первого уровня (см. рис. 8).

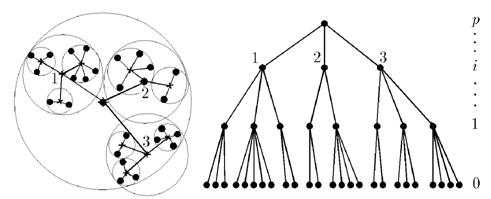
Рис. 8.

Так выглядит иерархическая таксономия, полученная методом скатывания мелких таксонов во все более крупные, который называют методом агломерации. Такое «генеалогическое» дерево позволяет видеть связи разных объектов и их групп друг с другом, что иногда бывает полезно при содержательном анализе массива данных. Иерархическое дерево может быть получено и другим путем — путем дробления крупных таксонов на более мелкие. Процедура такой таксономии практически совпадает с алгоритмом FOREL. Вначале определяется радиус 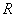наименьшей сферы, описывающей все 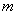точек. Эта сфера есть таксон верхнего корневого ( 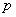-го) уровня. Затем радиус уменьшают и находят 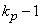таксон следующего 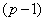-го уровня. Затем для объектов каждого из полученных таксонов процедура таксономии повторяется при еще меньшем радиусе. Некоторые из этих таксонов распадутся на несколько более мелких таксонов 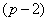-го уровня. Такой процесс дробления таксонов продолжается до тех пор, пока на некотором шаге не окажется, что количество таксонов стало равным числу объектов 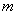. В результате получится дерево такого же вида, что и при агломерации.