2015-09-06
10895
рассмотрим двухатомную молекулу, состоящую из двух ядер на некотором расстоянии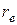 
, которое назовем равновесным, и обращающиеся вокруг ядер электроны. Связь между атомами в такой молекуле обусловлена электрическими силами взаимодействия между заряженными частицами (электронами и ядрами). Несмотря на то, что двухатомная молекула представляет собой некоторую динамическую систему из движущихся электронов и ядер, для простоты изучения картины вращения рассмотрим ее упрощенную модель. Согласно этой модели, молекула представляется в виде жесткого образования, по форме напоминающего гимнастическую гантель (см. рис.2.1).
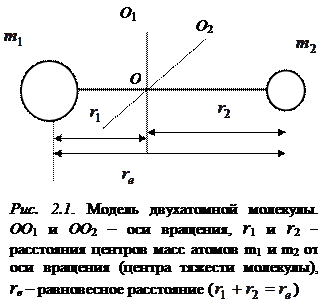
С точки зрения вращения она представляет собой жесткий ротатор (расстояние между атомами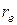 
постоянно). Вращается указанная система вокруг осей, проходящих через центр тяжести. Общее число таких осей равно трем. Однако вращение вокруг оси, проходящей через ядра атомов, не приводит к изменению энергий. Ядра считаются точечными, а массой электронов по сравнению с массой ядер пренебрегают, поэтому момент инерции вокруг указанной оси равен нулю. В двухатомной молекуле будем учитывать две различные оси вращения (OO 1 и OO 2), перпендикулярные оси молекулы, т. е. две вращательные степени свободы.
Для описания движения построенной модели двухатомной молекулы как целого необходимо получить выражения ее кинетической (Т) и потенциальной (V) энергий для данного вида движения (вращения). зная выражения, составим уравнение движения и решим его. В результате получим значения координат как функций времени, т. е. законы движения рассматриваемой модели.
Поскольку, для жесткого ротатора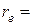 
const и потенциальная энергия V = const, которую можно положить равной 0, тогда полная энергия Е ротатора равна кинетической энергии вращающихся масс m 1 и m 2 вокруг одной из осей (OO 1 или OO 2), т. е.
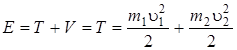(Е = Т, так как V = 0) (2.1)
где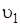 
и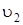 
– линейные скорости движения атомов, находящихся на расстоянии r 1 и r 2 от оси вращения. Вводя вместо линейной скорости угловую w(
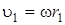и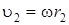 
), выражение (2.1) можно переписать следующим образом:
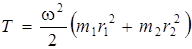, (2.2)
где выражение в скобках есть сумма моментов инерции I1 и I2 вращающихся атомов относительно оси вращения, r 1 и r 2 – расстояния массы атомов от оси вращения.
Можно показать, что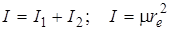 
, где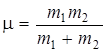 
– приведенная масса молекулы, а 
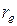– равновесное расстояние между атомами. Предоставляем это проделать читателю.
С учетом сказанного равенство (2.2) можно переписать следующим образом:
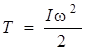, (2.3)
где I – момент инерции двухатомной молекулы. Таким образом, кинетическая энергия вращающейся молекулы пропорциональна квадрату угловой скорости и является функцией температуры. Это свидетельствует о том, что молекула может вращаться с любой скоростью w, определяемой температурой среды.
Поглощать или испускать радиацию могут те молекулы, у которых при вращении будет изменяться дипольный момент. Известно, что дипольный момент есть вектор. Он может изменяться и по величине, и по направлению. Так как расстояние между атомами в двухатомной молекуле принимается постоянным (жесткий ротатор), то при вращении молекулы дипольный момент изменяется только по направлению. Следовательно, поглощать или испускать радиацию будут те молекулы, которые обладают постоянным дипольным моментом. К таким относятся все молекулы, состоящие из неодинаковых атомов (например, СО NO, HCl и др.). У них центр тяжести положительных зарядов не совпадает с центром тяжести отрицательных зарядов. Все бездипольные молекулы, состоящие из одинаковых ядер, не обладают чисто вращательными спектрами поглощения и испускания. Эти молекулы имеют достаточно высокую симметрию (
), и у них центры тяжести положительных и отрицательных зарядов совпадают, т. е. отсутствует дипольный момент.
При комнатной температуре значительная часть молекул находится на сравнительно высоких (возбужденных) уровнях вращательной энергии. Распределены они по этим уровням в соответствии с законом Больцмана. Доля молекул, имеющих вращательную энергию в интервале от Е врдо Е вр + dЕ вр, выражается формулой
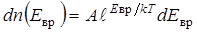, (2.4)
где dЕ вр = I wвр d wвр с учетом выражения (2.3), А – некоторая постоянная величина.
Пусть полное число молекул в единице объема с любыми вращательными энергиями равно n 0. Это же число молекул мы можем найти, пользуясь выражением (2.4), если проинтегрируем по всем вращательным энергиям от 0 до ¥.
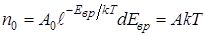, (2.5)
откуда A = n 0 /kT.
С учетом постоянной А формулу (2.4) можно переписать следующим образом:
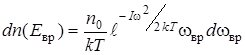. (2.6)
Классическое распределение интенсивностей во вращательной полосе совпадет с распределением молекул по различным вращательным состояниям, определяемым формулой (2.6), и графически представлено на рис. 2.2.
Так как по классической теории частоты wврмогут изменяться непрерывно, то полоса должна быть сплошной.
2.2. Квантовомеханический случай
Совсем по-иному подходит квантовая механика для нахождения энергии жесткого ротатора. Общий квантовомеханический подход для нахождения энергии заключается в решении уравнения Шредингера для жесткого ротатора
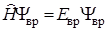, (2.7)
где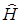 
– оператор Гамильтона для жесткого ротатора, ψвр – вращательная волновая функция, Е вр – собственное значение энергии оператора.
Учитывая, что для жесткого ротатора можно считать его потенциальную энергию V = 0, оператор Гамильтона будет равен только оператору кинетической энергии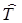 
такой системы. Уравнение Шрёдингера для стационарных состояний жесткого ротатора формально будет совпадать с уравнением движения свободной частицы с кинетической энергией Т и массой m:
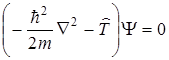, (2.8)
где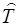 
– оператор кинетической энергии частицы, 
– оператор Лапласа. символ 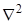(набла в квадрате) означает оператор, определяемый соотношением 
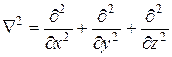. Для вращающегося ротатора это уравнение можно переписать следующим образом:
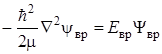, (2.9)
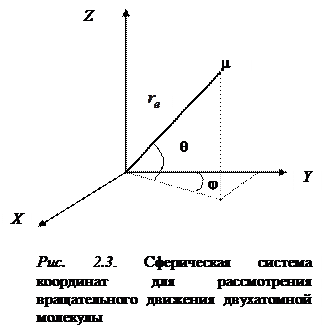
где m приведенная масса вращающейся молекулы. Если это уравнение переписать в сферических координатах r, q, j связанных с декартовыми координатами x, y, z соотношениями x = r sinqsinj, y = r sinqcosj, z = r cosj, то оно примет вид:
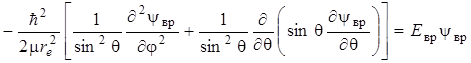. (2.10)
Здесь учтено то обстоятельство, что из общего выражения Лапласиана
,
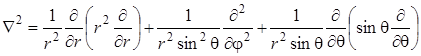первый член равен нулю, так как радиальная координата не изменяется в процессе вращения (жесткий ротатор). поэтому вращательная волновая функция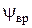 
зависит только от угловых координат q и j, а значение r равно 
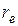.Таким образом, вращение двух масс m 1и m 2 вокруг одной из осей, проходящих через центр тяжести системы, мы заменяем вращением массы m. (приведенная масса молекулы), находящейся на расстоянии 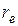от центра сферической системы координат (рис. 2.3).
Решение уравнения (2.9) можно представить в виде произведения двух функций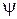 
(q, j) = f (q) j (j), где функции f и j зависят только от одной переменной. Учет граничных условий приводит к тому, что значение энергии E вр принимает только дискретные собственные значения:
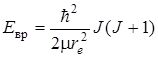, (2.11)
где J – вращательное квантовое число, принимающее значение
J = 0, 1, 2, 3, …
Выражение для энергии вращательных состояний молекулы можно получить гораздо проще, не решая уравнения Шрёдингера, а приняв во внимание только квантование момента вращения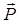 
.
Согласно законам квантовой механики для свободной системы (в нашем случае двухатомной молекулы) квантуется квадрат момента количества движения. Он принимает ряд дискретных значений, определяемых формулой
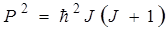,(2.12)
где J – вращательное квантовое число, принимающее целые значения
(J = 0,1, 2, 3, …).
Одновременно квантуется и проекция вращательного момента количества движения на выделенное направление относительно неподвижной (лабораторной) системы координат. Эту систему координат будем обозначать X¢, Y¢, Z¢ в отличие от системы координат X, Y, Z, cвязанной с молекулой. Проекция момента вращения относительно неподвижной оси (скажем, оси Z) равна:
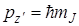, (2.13)
где mJ = J, J – 1, …, 0,…, –J принимает 2 J + 1 значений. Энергия вращающейся молекулы не зависит от проекции момента количества движения, а только от величины квадрата момента, т. е.
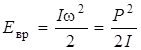(2.14)
Здесь учтено, что P = I w.
Так как энергия молекулы не зависит от проекции момента количества движения, а только от квадрата момента, то говорят, что вращательные уровни анергии свободной молекулы всегда вырождены со степенью вырождения g = 2 J + 1 (кроме уровня J = 0, для которого g = 1). Это связано с произвольностью ориентации момента количества движения относительно неподвижной системы координат.
Принимая во внимание выражение (2.12) для квадрата момента количества движения, равенство (2.14) можно переписать следующим образом:
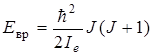, (2.15)
где значение момента инерции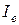 
относится к равновесному расстоянию между атомами (от латинского слова equilibrium – равновесие). Как видим, с учетом квантования квадрата момента количества движения, мы получили значение вращательной энергии, как и в (2.11). Согласно выражению (2.15) коэффициент при вращательном квантовом числе есть величина постоянная для данной молекулы. Обозначим этот коэффициент через 
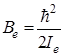, тогда формулу (2.15) можно переписать более просто:
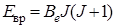, (2.16)
где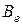 
– вращательная постоянная, относящаяся к минимуму кривой потенциальной энергии и соответствующая равновесному расстоянию между атомами. Эта постоянная полностью определяет значение вращательной энергии двухатомной молекулы. При изучении оптических спектров вращательную постоянную 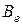обычно выражают в см–1 (в системе СИ она, как и энергия, выражается в Дж). Оценим для молекул H2 и HCl величину 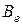в Дж и в см–1. для чего будем использовать ряд фундаментальных постоянных h = 6,626·10–34Дж·с; с= 2,998·108 м/с; I а.е.м. = 1,66·10–27 кг; Н¢=1,673×10–27 кг; Сl35 = 58,1×10–27 кг; re H2 = 0,074 нм; re HCl = 0,1275 нм.
Вычислим моменты инерции Ie:
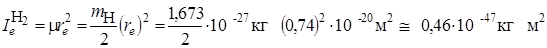
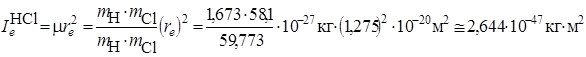Вычислим 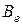вДж:
.
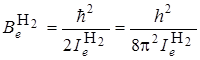Учитывая, что величина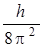 
постоянна и равна в системе СИ 5,56×10–69(Дж)2с2, то выражение для 
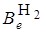будет иметь более простой вид:
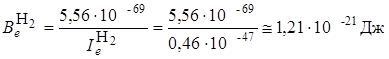
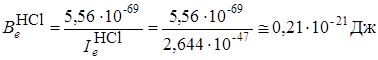
Вычислим 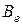в см–1 (так как 
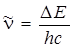, то для выражения 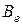в см–1 необходимо полученные величины выражать в системе СИ за исключением постоянной с, которую следует выражать в см×с–1). Итак, получим:
.
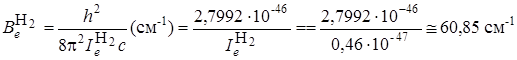
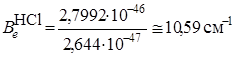Из оценки вращательной постоянной 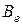видно, что чисто вращательные спектры располагаются в далекой ИК-области, соответствующей сантиметровому и миллиметровому диапазонам.
Так как значения вращательной энергии квадратично зависят от вращательного квантового числа J, то уровни вращательной энергии представляют собой расходящуюся последовательность.
В табл. 2.1 приведены значения Е вр в зависимости от вращательного квантового числа J, а в табл. 2.2 межъядерные расстояния двухатомных молекул. Чтобы описать спектр поглощения или испускания, необходимо знать вероятности переходов между уровнями энергии и правила отбора.
Таблица 2.1
Значения вращательной энергии Е вр двухатомной молекулы
в зависимости от J
| Е вр | 2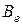
| 6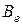
| 12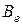
| 20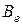
| 30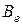
| 42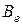
| 56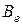
| 72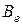
| |
| J |
Таблица 2.2
Вращательные постоянные 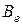, межъядерные расстояния re
