2015-10-14
215
Если характеристический полином САУ имеет вид
,
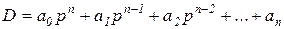то САР устойчива тогда, и только тогда, если определитель Гурвица
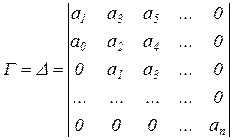
и все его диагональные миноры положительны, откуда следует, что если:
1) 
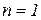=> уравнение: 
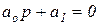. Определитель Гурвица: 
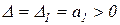при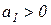 
, то есть условие устойчивости: 
, ;
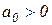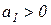2) 
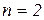=> уравнение: 
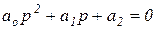. Определители Гурвица: 
, 
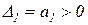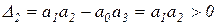, так как 
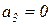, то есть условие устойчивости: , , 
;
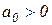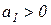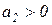3) 
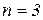=> уравнение: 
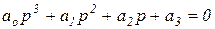. Определители Гурвица: , , 
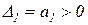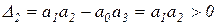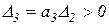, условие устойчивости: , , , 
, 
.
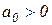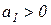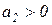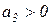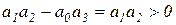При увеличении порядка системы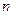 
число подобных неравенств, требующих проверки, и их сложность стремительно растут, например, для системы порядка четыре необходимо проверить уже более сложное неравенство 
.
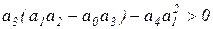Частотные критерии устойчивости
