2015-10-14
735
Годограф характеристического полинома n -го порядка с положительными коэффициентами (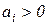
) устойчивой САУ должен, начинаясь на положительной вещественной полуоси, последовательно пройти n квадрантов, поворачиваясь против часовой стрелки. Приращение аргумента годографа при этом составляет 
.
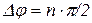Критерий Найквиста – позволяет исследовать устойчивость замкнутой системы (всей САУ) по частотной характеристике разомкнутой системы.
Если разомкнутая система устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф устойчивой разомкнутой системы «не охватывал» точку с координатами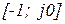 
.
Если разомкнутая система неустойчива и имеет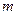 
неустойчивых корней, тогда для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф Найквиста разомкнутой системы охватил точку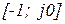 
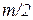раз.
Уточним понятие «охват точки» 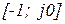годографом Найквиста с помощью правила переходов:
- положительным считается переход годографа левее 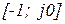снизу вверх;
- отрицательным считается переход годографа левее 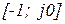сверху вниз;
|
|
|
(
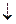– отрицательный, 
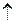– положительный).
Неохват означает, что сумма переходов равна нулю.
Охват означает, что положительных переходов больше, чем отрицательных.
Если годограф начинается на отрицательной полуоси, то начальный переход при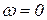 
считается за 1/2 перехода.
Отметим, что устойчивость линейной САУ можно оценить также и по ее временному графику.
Для этого необходимо задать отличные от нуля начальные условия или оказать на систему ступенчатое или импульсное воздействие, а затем проанализировать характер ее движения.
В данной работе будем рассматривать системы, характеристический полином которых имеет степень не более 3.
Стенд для исследования устойчивости систем показан на рис. 1.
В нем использовано динамическое звено, позволяющее моделировать любую дробно-рациональную передаточную функцию вида
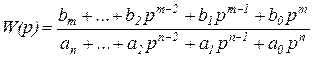при обязательном условии 
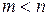. (1)
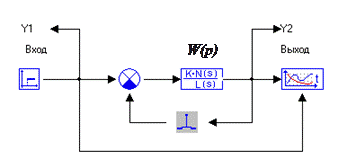
Рис. 1
В данном случае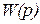 
– передаточная функция разомкнутой системы.
Для удобства замыкания-размыкания отрицательной обратной связи в ее цепь установлен ключ, который «двойным кликом мыши» переходит из замкнутого в разомкнутое состояние и наоборот.
Задание коэффициентов числителя и знаменателя производится в том порядке, как они расположены в выражении (1).
Для построения годографов Михайлова и Найквиста используются блоки «В память», обозначенные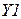 
(Вход) и 
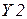(Выход).
Контрольные вопросы
1 Что понимают под устойчивостью САУ в малом и в большом?
2 Что такое характеристическое уравнение?
3 Какой вид имеют корни характеристического уравнения?
|
|
|
4 Чем отличаются правые и левые корни характеристического уравнения?
5 Сформулируйте условие устойчивости систем по Ляпунову.
6 Что такое граница устойчивости?
7 Что такое критерии устойчивости?
8 Сформулируйте необходимое условие устойчивости САУ.
9 Сформулируйте критерий Гурвица.
10 В чем достоинства и недостатки алгебраических критериев устойчивости?
11 Что называется частотными критериями устойчивости САУ?
12 В чем преимущество частотных критериев устойчивости перед алгебраическими:
13 Сформулируйте критерий устойчивости Михайлова.
14 Сформулируйте критерий устойчивости Найквиста.
15 В чем особенность использования критерия Найквиста для астатических САУ?
