Силы в электрических полях

2.7.1. Пондеромоторные силы.

В электрических полях на диэлектрики и проводники действуют силы, которые называют пондеромоторными, т.е. (в переводе) силами, действующими на весомые тела. Термин пондеромоторные силы безусловно устарел, поскольку был введен в то время, когда в физике признавалось существование невесомых субстанций (например, теплород, эфир, электрические и магнитные жидкости). Теперь известно, что невесомых субстанций не существует, но этот термин по-прежнему используется. Механические явления, такие как растягивание заряженной поверхности, механические напряжения в диэлектрических слоях, втягивание диэлектрика в конденсатор, взаимодействие проводников с током, механическое действие оптического излучения на тела, объясняются пондеромоторными силами. Природа этих сил вполне определена – они возникают при воздействии электромагнитного поля на электрические заряды.

Рассмотрим возникновение и действие пондеромоторных сил применительно к электростатике.

Поскольку электростатическое поле потенциально, то для любой системы электрических зарядов можно записать

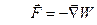. (7.1)

Сила, действующая на какой-либо заряд, определяется, очевидно, напряженностью 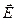того поля, в которое помещен этот заряд (но не того поля, которое возбуждается им самим):

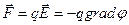, (7.2)

т.к.

.

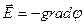Если заряд непрерывно распределен по объему с плотностью 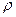, то сила, действующая на элемент заряда 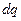, равна

.

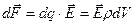Можно также ввести объемную плотность сил, которая равна

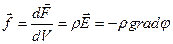. (7.3)

Силы, действующие в поляризованном диэлектрике.

Силы, действующие на электрические диполи в веществе, деформирующие и ориентирующие их в пространстве, относятся к пондеромоторным силам.

Ранее в §1.7 мы получили выражение (7.13) для силы, действующей на одиночный диполь в электрическом поле. Причем, как мы выяснили, сила, действующая в однородном поле на отдельный диполь, равна нулю.

Рассмотрим теперь силы, действующие в объеме диэлектрика, помещенного в электрическое поле. Сила, приложенная к элементу объема 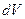диэлектрика, равна сумме сил, действующих на элементарные диполи внутри рассматриваемого объема :

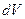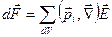, (7.4)

причем суммирование ведется по всем элементарным диполям, находящимся в объеме 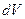. Так как элемент объема 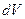мал, то вектор напряженности электрического поля 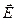- медленно меняющаяся в пределах этого объема величина. Поэтому, вводя вектор поляризации 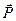, можем записать

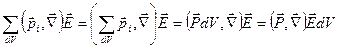. (7.5)

Отсюда объемная плотность сил в диэлектрике:

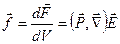. (7.6)

Для однородного диэлектрика справедливо соотношение

,

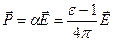тогда получаем выражение для объемной плотности сил в виде:

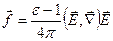. (7.7)

Воспользуемся тождеством из векторной алгебры {см. (7.12), §1.7},

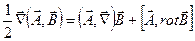записанным для :

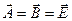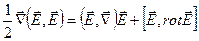. (7.8)

Поскольку для электростатического поля 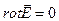, получаем теперь для объемной плотности пондеромоторных сил:

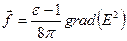. (7.9)

Если рассматриваемый диэлектрик однородный (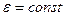, 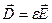), то

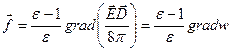. (7.10)

Формулы (7.9) и (7.10), выражающие объемную плотность сил справедливы как для абсолютно жестких, так и для упруго деформируемых диэлектриков. Последнее утверждение справедливо лишь при условии, что поляризованность диэлектрика (вектор поляризации 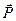) линейно зависит от его массы, т.е. дипольные моменты молекул и атомов при сжатии и растяжении элемента объема не изменяются.

Если диэлектрическая проницаемость не постоянна 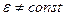, и мы имеем дело с сжимаемыми диэлектриками, то определение пондеромоторных сил довольно сложно. Общий метод вычисления пондеромоторных сил дает термодинамика - термодинамика диэлектриков. Определяются термодинамические функции диэлектриков - свободная энергия, термодинамический потенциал, энтальпия. В данном курсе мы не будем этим заниматься.

2.7.2. Силы, действующие на поверхностные заряды.

Ранее мы уже затрагивали этот вопрос. Если имеется замкнутая проводящая поверхность, заряженная с поверхностной плотностью 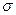, то электрическое поле известно по обе стороны, причем 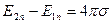, а на самой поверхности электрическое поле не определено. В результате взаимодействия поверхностных зарядов поверхность проводника растягивается. Как найти силу, действующую на единицу поверхности?

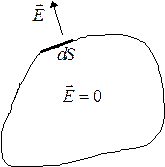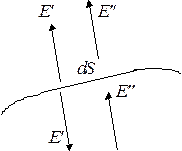Рассмотрим уединенный проводник. Выделим элемент поверхности :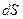

1) поле с внешней стороны выделенного элемента поверхности равно ;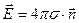

2) поле внутри .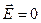

Поле внутри и снаружи проводника можно рассматривать как суперпозицию полей, создаваемых самим элементом поверхности 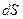, т.е. 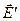, и всеми остальными зарядами, находящимися на поверхности 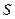: 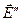. Поле 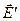одинаково по величине по обе стороны от площадки 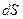, но имеет противоположные направления. Поле 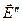одинаково по модулю и направлению над и под площадкой .

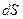Тогда с внешней стороны 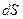имеем

.

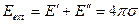С внутренней стороны

.

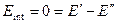Из этих соотношений находим поле, в месте расположения элемента .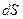

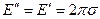. (7.11)

Сила, действующая на заряд 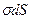, находящийся на поверхности 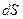, определяется величиной поля 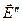и равна

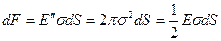. (7.12)

Пондеромоторная сила, действующая на единицу поверхности (поверхностная плотность пондеромоторных сил):

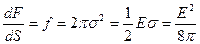. (7.13)

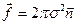. (7.14)

2.7.3. Определение пондеромоторных сил через энергию электрического поля.

Один из общих способов определения сил через производную от энергии системы:

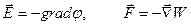. (7.15)

Пример: силы, действующие на пластины плоского конденсатора. Энергия его электрического поля:

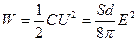. (7.16)

Здесь градиент энергии следует понимать как её изменение на длине 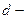расстоянии между обкладками конденсатора.

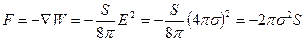. (7.17)

Знак “минус” в последнем выражении показывает, что между обкладками действует сила притяжения.