Предполагая, что на периферии диска (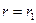 ) и на расточке (
) и на расточке (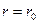 ) заданы радиальные напряжения, принимаем, что граничные условия соответствуют условиям (6). Подчиняя напряжения (9) при
) заданы радиальные напряжения, принимаем, что граничные условия соответствуют условиям (6). Подчиняя напряжения (9) при 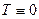 этим граничным условиям, получаем
этим граничным условиям, получаем
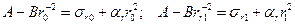 . (18)
. (18)
Определив постоянные А и В из (18) и подставив их выражения в уравнения (9) и (10), получим
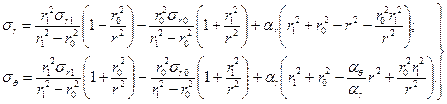 (19)
(19)
Первые члены в правых частях уравнений (19) соответствуют напряжениям, обусловленным нагрузкой, вторые члены – нагрузкой на расточке диска, а третьи члены соответствуют напряжениям в свободном вращающемся диске без краевых нагрузок. Составляющие окружного напряжения возрастают вблизи расточки и на самой расточке достигают максимального значения.
Суммарное напряжение 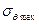 на расточке найдем из (19), приняв
на расточке найдем из (19), приняв 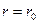 , т.е.
, т.е.
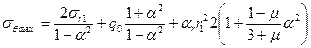 , (20)
, (20)
где 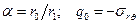 .
.
Из последнего соотношения видно, что размер отверстия оказывает существенное влияние на максимальное напряжение – при увеличении 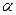 все три составляющие напряжения растут. Третье слагаемое при увеличении
все три составляющие напряжения растут. Третье слагаемое при увеличении 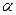 от 0 до 1 возрастает в отношении
от 0 до 1 возрастает в отношении 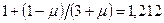 , т.е. на 21 %.
, т.е. на 21 %.
Сравним максимальное напряжение 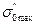 в диске с малым центральным отверстием при
в диске с малым центральным отверстием при 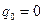 с напряжением
с напряжением 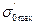 в центре сплошного диска. Примем
в центре сплошного диска. Примем 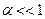 . Из уравнений (20) и (17) при
. Из уравнений (20) и (17) при 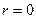 следует
следует
|
|
|
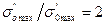 ,
,
т.е. центральное отверстие малого диаметра в сплошном диске приводит к увеличению максимального напряжения в 2 раза. Малое отверстие в диске является источником концентрации напряжений с коэффициентом концентрации 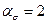 . По мере роста диаметра расточки наблюдается дополнительное увеличение максимального напряжения на поверхности отверстия согласно уравнению (20).
. По мере роста диаметра расточки наблюдается дополнительное увеличение максимального напряжения на поверхности отверстия согласно уравнению (20).
Очевидно, что распределение динамических напряжений в диске постоянной толщины с отверстием носит неравномерный характер, и окружные напряжения возрастают по мере приближения к расточке, достигая максимального значения на поверхности центрального отверстия. Типичные эпюры напряжений в диске с отверстием представлены на рис. (5).
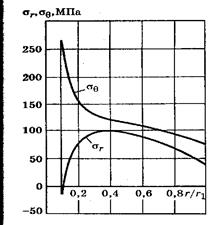
Рис. 5 Распределение напряжений в диске с центральным отверстием при 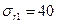 МПа;
МПа; 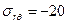 МПа;
МПа; 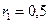 м;
м; 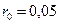 м;
м; 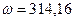 рад/с;
рад/с; 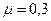
 2015-10-16
2015-10-16 905
905








