| Комбинаторика | ||
| Комбинаторика – раздел математики, в котором изучаются способы выбора и размещения элементов некоторого конечного множества на основании некоторых условий. Выбранные (или выбранные и размещенные) группы элементов называются соединениями. Если все элементы полученного множества разные – получаем соединения без повторений, а если в полученном множестве элементы повторяются, то получаем соединения с повторениями | ||
| Перестановки | ||
| Перестановкой из n элементов называется любое упорядоченное множество из n элементов. Иными словами, это такое множество, для которого указано, какой элемент находится на первом месте, какой на втором, ………….., какой на n – м. | ||
Формула перестановок числа (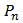 ) ) | Пример | |
(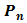 ) = n! Где n! = 1*2*3*…………….* n (читается: «Эн акториал») ) = n! Где n! = 1*2*3*…………….* n (читается: «Эн акториал») | Количество различных шестизначных чисел, которые можно составить из цифр 1,2,3,4,5,6, не повторяя эти цифры в одном числе, равно 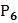 = 6! = 1*2*3*4*5*6 = 720 = 6! = 1*2*3*4*5*6 = 720 | |
| Размещение | ||
| Размещением из n элементов по k называется любое упорядоченное множество из k элементов, состоящее из элементов n – элементарного множества. | ||
Формула числа размещений (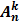 ) ) | Пример | |
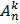 = = 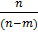 или или 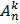 = n(n -1)(n – 2)…… ……. (n –k + 1) = n(n -1)(n – 2)…… ……. (n –k + 1) | Количество различных трехзначных чисел, которые можно составить из цифр 1,2,3,4,5,6, если цифры не могут повторяться, равно 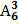 = = 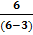 = =  = = 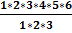 = 4*5*6 = 120 = 4*5*6 = 120 | |
| Сочетания | ||
| Сочетание без повторений из n элементов по k называется любое k – элементное подмножество n – элементного множества. | ||
Формула числа сочетаний 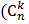 ) ) | Пример | |
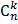 = = 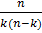 (по определению считают, что (по определению считают, что 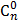 = 1) = 1) | Из класса, состоящего из 25 учащихся, можно выделить 5 учащихся для дежурства по школе 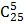 способами, то есть способами, то есть 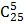 = = 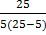 = = 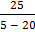 = = 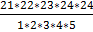 = 53130 = 53130 | |
| Некоторые свойства числа сочетаний без повторений | ||
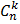 = = 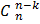 (в частности, (в частности, 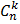 = = 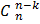 = = 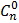 = 1) = 1) 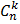 + + 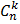 + 1 = + 1 = 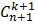 | ||
| Схема решений комбинаторных задач | ||
| Выбор правила | ||
| Правило суммы | Правило произведения | |
| Если элемент А можно выбрать m способами, а элемент B–n способами, то А и В можно выбрать m + n способами. | Если элемент А можно выбрать m способами, а после этого элемент В-n способами, то А и В можно выбрать m*n способами. | |
| Выбор формулы | ||
Учитывается ли порядок следования элементов в соединении?
ДА НЕТ
Все ли алименты
входят в
соединение?
ДА НЕТ
 2015-10-16
2015-10-16 929
929








