| Определение
| Пример
| Теоретико множественная иллюстрация
|
| 1.Противоположное событие
|
Событие 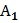 называется противоположным событию А, если оно происходит тогда, когда не происходит событие А.
Вероятность противоположного события: Р называется противоположным событию А, если оно происходит тогда, когда не происходит событие А.
Вероятность противоположного события: Р 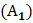 = 1 – Р(А) = 1 – Р(А)
| Событие А– выпал «герб»при подбрасывании монеты, тогда событие 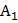 – не выпал «герб» при подбрасывании монеты (то есть выпало число). – не выпал «герб» при подбрасывании монеты (то есть выпало число).
|
|
| Если вероятность купить исправный прибор равна 0,95, то вероятность купить не исправный прибор равна: 1 – 0,95 = 0,05
|
| 2.Сумма событий
|
| Суммой (или объединением) событий А и В называется событие А + В (другое обозначение А U В), которое происходит тогда и только тогда, когда происходит событие А или событие В.
| Из колоды карт наугад вынимают 1 карту. Рассмотрим события: А- вынули бубновою карту, В – вынули червовую карту.
Тогда события А + В– вынули или бубновою или червовую карту (то есть карту красной масти).
|
|
| 3.Производение событий
|
| | | | |
| Два случайных события А и В называются несовместимыми, если произведение является невозможным событием, то есть
А*В =
| При бросании игрального кубика рассматривают события: А– выпало четное число очков, В – выпало 1 очко, С – выпало число очков, кратное 3
События Аи Ви события Ви С – несовместимы (не могут происходить одновременно). События Аи С –совместимые (могут происходить одновременно, если выпадает 6 очков).
|
|
| 5.Вероятность суммы двух несовместимых событий
|
| Если события А и В несовместимые, то Р(А + В) = Р(А) + Р(В), то есть вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий.
|
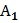 называется противоположным событию А, если оно происходит тогда, когда не происходит событие А.
Вероятность противоположного события: Р
называется противоположным событию А, если оно происходит тогда, когда не происходит событие А.
Вероятность противоположного события: Р 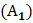 = 1 – Р(А)
= 1 – Р(А)
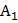 – не выпал «герб» при подбрасывании монеты (то есть выпало число).
– не выпал «герб» при подбрасывании монеты (то есть выпало число).
 2015-10-16
2015-10-16 471
471








