Задача 1. Тело брошено вверх под углом a = 60° к горизонту с начальной скоростью u0 = 30 м/с (рис. 3.1). Определить скорость тела через время t = 2 с, тангенциальное ускорение в этот момент времени и полное время движения тела.
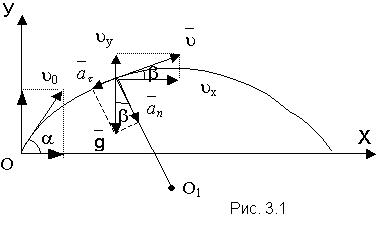 |  | Решение. Систему отсчета связываем с Землей. Начало системы координат помещаем в точку, из которой тело начинает движение. Ось ОУ направляем вертикально вверх, ось ОХ горизонтально. Зависимость вектора скорости 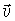 от времени имеет вид от времени имеет вид 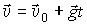 . Запишем проекции вектора . Запишем проекции вектора 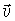 по осям ОХ: uХ = uОХ; ОУ: uУ = uОУ – gt,где uОХ = uО cosa, uОУ = uО sina. по осям ОХ: uХ = uОХ; ОУ: uУ = uОУ – gt,где uОХ = uО cosa, uОУ = uО sina. |
Найдем модуль вектора скорости в соответствии с чертежом (рис. 3.1)
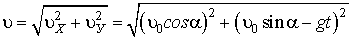 . (3.3)
. (3.3)
Угол наклона b вектора 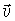 к горизонту определим через
к горизонту определим через
tgb = uУ /uХ. (3.4)
Подставив числовые данные в (3.3) и (3.4), получим:
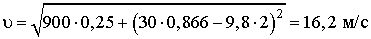 ;
;
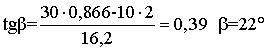 .
.
Как видно из чертежа (рис. 3.1), тангенциальное ускорение: 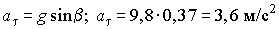 . Для нахождения полного времени движения tП используем уравнение координаты у = у0 + Sу. Так как у0 = 0 и у = 0, то и Sу = 0. Зависимость вектора перемещения от времени имеет вид
. Для нахождения полного времени движения tП используем уравнение координаты у = у0 + Sу. Так как у0 = 0 и у = 0, то и Sу = 0. Зависимость вектора перемещения от времени имеет вид
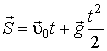 . (3.5)
. (3.5)
Проекция вектора  на ось ОУ:
на ось ОУ: 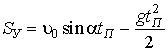 . Из этого соотношения, подставив SУ = 0, найдем:
. Из этого соотношения, подставив SУ = 0, найдем:
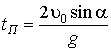 . (3.6)
. (3.6)
Выполним расчет: 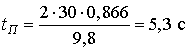 .
.
Ответ: 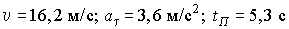 .
.
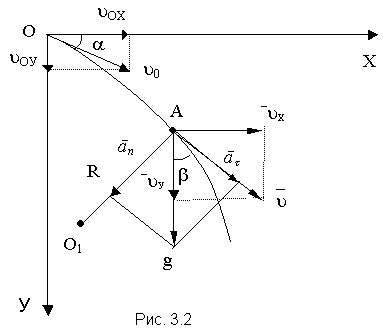
Задача 2. Тело брошено вниз под углом a = 30° к горизонту с начальной скоростью u0 = 20 м/с. Определить проекцию вектора перемещения на ось ОХ и радиус кривизны траектории через t = 0,5 с.
 |  | Решение. Зависимость вектора перемещения от времени имеет вид 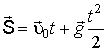 . (3.7) Проекция вектора . (3.7) Проекция вектора 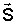 на ось ОХ: на ось ОХ:  . Рассчитаем SХ: . Рассчитаем SХ: 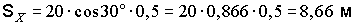 . . |
Для определения радиуса кривизны траектории в точке А воспользуемся формулой 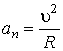 , где u – модуль скорости тела в точке А,
, где u – модуль скорости тела в точке А, 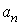 – центростремительное (нормальное) ускорение. Зависимость вектора скорости u от ее проекций uХ и uУ:
– центростремительное (нормальное) ускорение. Зависимость вектора скорости u от ее проекций uХ и uУ: 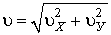 , где uХ = uО cosa, uУ = uО sina + gt. Центростремительное ускорение, как видно из рис. 3.2,
, где uХ = uО cosa, uУ = uО sina + gt. Центростремительное ускорение, как видно из рис. 3.2, 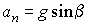 .
.
Угол b выразим через u и uХ: sinb = uХ / u. Произведем расчеты:
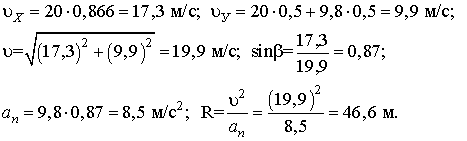
Ответ: SX = 8,66 м; R = 46,6 м.
 2015-10-16
2015-10-16 1371
1371








