2015-10-16
514
Будем рассматривать пружину, как винтовую линию с пренебрежимо малым шагом, таким, что каждый ее виток перпендикулярен силам, действующим на пружину. Момент сил, действующий в любом сечении витка пружины в таком случае постоянной величиной, равной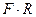 
, где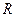 
- радиус пружины. Вектор момента сил направлен по касательной к витку, и, следовательно, вызывает деформацию чистого кручения витков пружины. Следствием этой деформации будет изменение длины пружины, т.е. ее линейная деформация. Проследим геометрическую связь деформации кручения бесконечно малого элемента витка пружины 
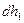и удлинения пружины 
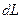. Рассмотрим бесконечно малый вектор перемещения 
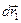точки приложения силы 
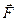, находящейся на оси пружины (см. рис 10).
Этот вектор направлен перпендикулярно вектору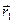 
, соединяющему элемент витка с точкой приложения силы. Величина его равна 
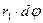, где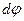 
- угол кручения элемента витка. Направление вектора перемещения образует с осью пружины угол 
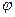. На рис. 10 изображен также вектор перемещения 
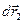точки приложения силы при кручении элемента витка, расположенного на одном диаметре с первым элементом и имеющим такую же длину. По этой причине модули обоих векторов перемещений одинаковы и мы обозначим их через 
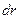. Видно, что сумма этих векторов направлена по оси пружины и ее величина равна 
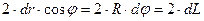. Таким образом, перемещение точки приложения силы при кручении одного элемента витка на угол 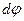выражается формулой 
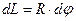. Угол кручения вычислим с помощью соотношения 6: 
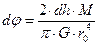. Полную линейную деформацию 
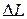пружины с общей длиной всех 
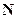витков 
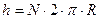можно получить с помощью интегрирования:
,
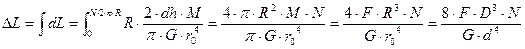где d – диаметр проволоки пружины, D – диаметр пружины, N - количество витков.
Следовательно, жесткость пружины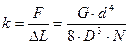 
. (8)
Из формулы (8) вытекает связь модуля сдвига и жесткостью пружины:
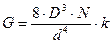(9)
Для экспериментального определения жесткости пружины в данной работе изучаются свободные колебания груза известной массы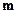 
, подвешенного на пружине (пружинный маятник). Зависимость отклонения от равновесного положения груза от времени 
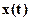подчиняется следующему уравнению динамики:
.
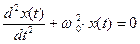Решение этого уравнения, как следует из теории, имеет вид: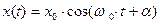 
,
где амплитуда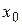 
и начальная фаза 
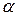определяются начальными условиями; 
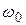¾ угловая частота крутильных колебаний, период которых Т равен: 
,
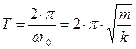откуда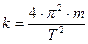 
. Подставляя этот результат в формулу (9), получаем следующую расчетную формулу:
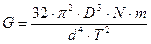(10)
