На практике встречается задача, когда закон распределения исследуемой случайной величины считается известным с точностью до 1-го или нескольких неизвестных параметров этого распределения. Возникает проблема оценивания этих параметров по выборке.
Неизвестные параметры 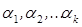 распределения случайной величины x с помощью статистик
распределения случайной величины x с помощью статистик 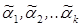 , т.е. сделаем точные оценки, для которых можно говорить об общих свойствах таких оценок, т.е. состоятельности, несмещенности и эффективности.
, т.е. сделаем точные оценки, для которых можно говорить об общих свойствах таких оценок, т.е. состоятельности, несмещенности и эффективности.
1. Метод моментов
Пусть закон распределения исследуемой случайной величины зависит от параметров 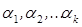 , численные значения которых подлежат оценки. Метод моментов заключается в следующем.
, численные значения которых подлежат оценки. Метод моментов заключается в следующем.
1) Методом теории вероятности первый k теоретических моментов начальных или центральных через параметры распределения.
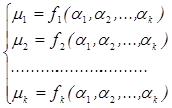
Разрешим полученную таким образом систему уравнений относительно параметров, получим новую систему.
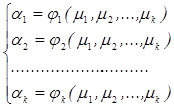
Получим требуемые оценки, подставляя вместо неизвестных теоретических моментов 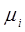 , их соответствующие статистические оценки
, их соответствующие статистические оценки 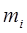 .
.
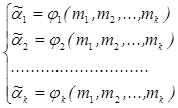
Если система, полученная на первом этапе не разрешается аналитически, то она решается численно после замены 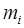 на
на 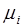 .Если функции
.Если функции 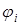 непрерывные, то из их состоятельности выборочных моментов
непрерывные, то из их состоятельности выборочных моментов 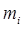 следует состоятельность полученных оценок параметров
следует состоятельность полученных оценок параметров 
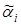 .
. 
2) Метод максимального правдоподобия.
Более точным с точки зрения эффективности является данный метод, но на практике приводит к решению более сложных задач вычислительного характера.
Пусть функция f (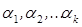 )-есть плотность распределения исследуемой случайной величины, тогда функцией правдоподобия называется статистика
)-есть плотность распределения исследуемой случайной величины, тогда функцией правдоподобия называется статистика
L (x1,x2,…xn; 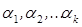 )=
)= 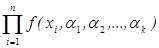 .
.
Выборочные значения xi независимы, поэтому функция правдоподобия является плотностью совместного распределения выборки. Метод максимального правдоподобия заключается в отыскании максимума функции правдоподобия. На практике удобнее максимизировать не саму функцию правдоподобия, а ее логарифм.
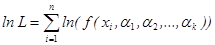
Продифференцируем по параметрам k -раз, мы получим частные производные
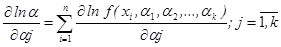
Решая эту систему из k -уравнений, получаем искомые оценки 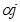 , т.е. система решается аналитически и численно, в последнем случае вместо выборочных значений xi подставляют перед решением наблюдаемые выборочные значения и в результате численного решения получаем наблюдаемые значения, интересующих нас параметров.
, т.е. система решается аналитически и численно, в последнем случае вместо выборочных значений xi подставляют перед решением наблюдаемые выборочные значения и в результате численного решения получаем наблюдаемые значения, интересующих нас параметров.
Пример: Рассмотрим нормальное распределение, закон Гаусса.
Найдем для данной функции функцию правдоподобия.
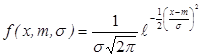
Найти функцию правдоподобия
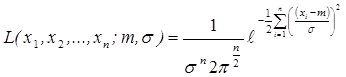
Пусть в результате испытаний величина x приняла n -значений
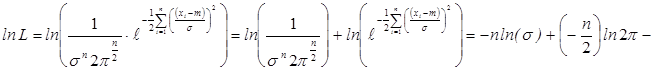

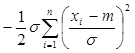 ;
;
Дифференцируем
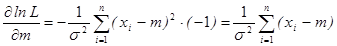
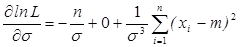



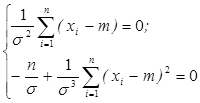

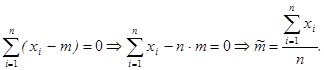
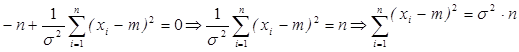 ;
;
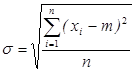 ;
; 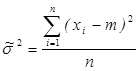 .
.
Мы получили оценки математического ожидания и дисперсии, ими являются выборочные средние и дисперсия.
 2015-10-16
2015-10-16 497
497








