2015-10-16
3050
Допустим, что из теоретических соображений, удалось установить какое именно распределение имеет случайная величина. Пусть закон распределения x содержит неизвестный параметр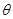 
, требуется приближенно оценить этот параметр. Пусть для получения значения величины проведено x -независимых испытаний, так, что их результаты x 1, x 2,… xn образуют случайную выборку. Полученные результаты будем рассматривать как n -независимых случайных величин, оценкой параметра 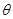называется функция f (x 1, x 2,… xn) от случайной выборки, которая дает приближенное значение оцениваемого параметра. Функция f (x 1, x 2,… xn) является случайной величиной.
Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.
Состоятельность и несмещенность оценок
Для того чтобы статистические оценки давали хорошие приближения, оцениваемых параметров они должны удовлетворять определенным требованиям. Пусть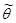 
-есть статистическая оценка параметра 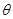теоретического распределения. Допустим, что в серии n -испытаний по выборке объема n найдена оценка 
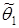в другой серии 
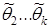. Эти числа будут различными между собой, оценку мы можем рассматривать как случайную величину, а все данные числа 
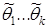, как ее возможные значения. Если оценка 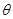дает приближенное значение параметра 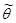с избытком, тогда каждое найденное 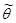> 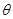, 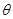- истинное, теоретическое значение параметра.
В этом случае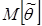 
> 
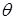, если 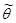дает оценку с недостатком, то 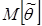< 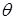. Используя оценки, для которых математическое ожидание не равно истинному значению мы приведем к систематическим ошибкам, причем одного знака, поэтому требуют, чтобы математическое ожидание было равно .
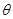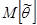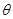= (1)
Оценка 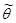называется несмещенной, если ее 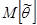равно теоретическому оцениваемому значению 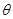, т.е. выполняется равенство (1).
Оценка называется асимптотически несмещенной, если
;
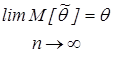Несмещенность оценки означает, что если мы будем получать ожидаемые значения на различных ожиданиях выборки, то центр тяжести этих значений будет практически совпадать с теоретическим значением, что свидетельствует об отсутствии систематической шибки при оценивании. Асимптотическая несмещенность означает исчезновение асимптотической ошибки при n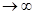 
. Т.е. оценка несмещенная на выборках достаточно большого объема. Возможные значения 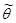могут быть сильно рассеяны вокруг своего среднего значения, т.е. дисперсия может быть значительной. Оценка 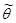называется эффективной, если она имеет наименьшую среднеквадратическую ошибку среди всех других возможных оценок данной характеристики 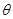.Т.е., если оценка несмещенная, то эффективность означает минимум ее дисперсии.
Эффективная оценка- наиболее точная оценка из всех возможных.
При рассмотрении выборок большого объема к статистическим оценкам предъявляется требование состоятельности. Оценка 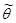называется состоятельной, если она сходится по вероятности к оцениваемому теоретическому значению .
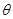Для любого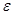 
<0, выполняется равенство
;
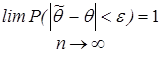Состоятельность означает, что при неограниченном увеличении объема выборки наблюдаемые значения статистики 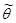практически достоверно попадает в 
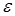- окрестность оцениваемого значения .
;
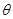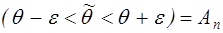Т.е. событие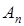 
достоверно. Если дисперсия оценки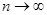 
;
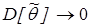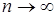
-это является необходимым условием состоятельности.
Хорошая оценка должна быть состоятельной, несмещенной и эффективной.
