Пусть зависимость между переменными величинами x и y задана, вычислены групповые средние, соответствующие каждому значению xi, а точки Ai с координатами 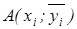 располагаются по параболе 2-го порядка, т.е. уравнение параболы будем искать в виде y=a 0 +a 1 x+a 2 x2. Из всех парабол того же вида, искомая ближе всего к точкам Ai, причем каждая точка имеет частоту nxi- раз, т.е. сколько раз встречается распределение xi. Следовательно, для искомой параболы минимальна сумма квадратов разности ординат точек Ai, имеющих с ними одинаковые абсциссы Ai, где
располагаются по параболе 2-го порядка, т.е. уравнение параболы будем искать в виде y=a 0 +a 1 x+a 2 x2. Из всех парабол того же вида, искомая ближе всего к точкам Ai, причем каждая точка имеет частоту nxi- раз, т.е. сколько раз встречается распределение xi. Следовательно, для искомой параболы минимальна сумма квадратов разности ординат точек Ai, имеющих с ними одинаковые абсциссы Ai, где 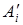 имеет координаты:
имеет координаты:
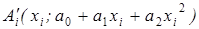 ;
;
Следовательно, расстояние (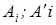 )-это есть
)-это есть
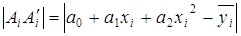 ;
;
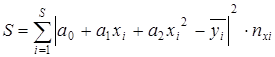 ;
;
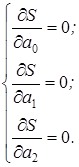
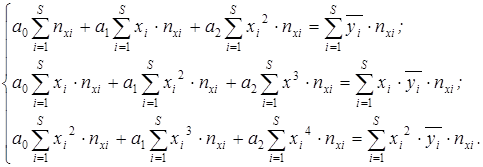
Пример: Дана корреляционная таблица зависимости урожайности от глубины орошения.
| Итого: | ||||||||
| - - - - | - | - - | |||||||
| Итого: |
c =14; k =2
| xi | nxi | 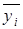
| xi×nxi | xi2×nxi | xi3×nxi | xi4×nxi | 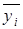 × nxi × nxi
| xi × 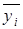 × nxi × nxi
| xi 2× 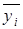 × nxi × nxi
|
| 10,4 14,67 14,286 13,67 | |||||||||
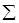
|
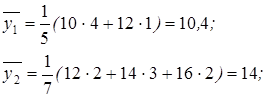
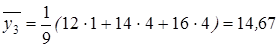 ;
;
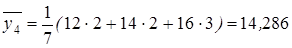 ;
;
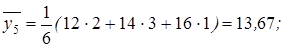
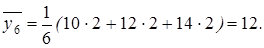
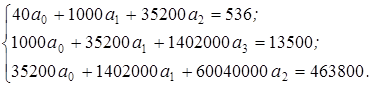
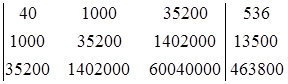
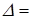
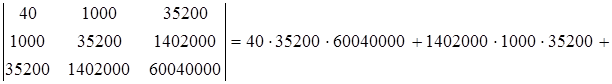
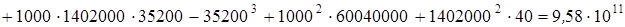 ;
;
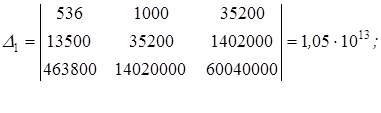
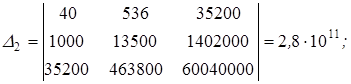
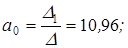
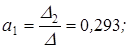
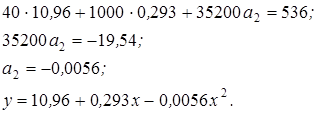
 2015-10-16
2015-10-16 319
319








