2015-10-16
2625
Линейная корреляционная зависимость- это вид линейной зависимости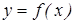 
, корреляционная зависимость между x и y. При нахождении корреляционной зависимости на подвергается анализу расположение точек на числовой плоскости, после выбора функции
;
.
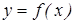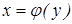Задача сводится к нахождению параметров искомой функции по данным корреляционной таблицы. Наиболее важные - линейные зависимости. Рассмотрим и зависимость y на x. В прямоугольной системе координат построим точки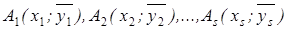 
. Предположим, что между переменными x и y существует линейная корреляционная зависимость y на x.
 |
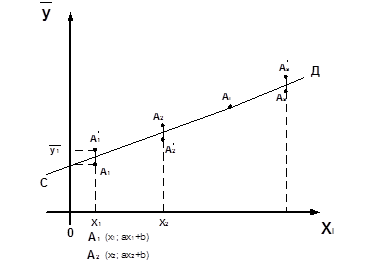Искомой прямой служит та, которая в смысле принципа наименьших квадратов ближе других расположена к точкам A 1, A 2,…, As,причем т. A 1 учитывается nx 1 -раз,т.е. сколько раз встречаются в распределении соответствующие значения xi. Прямая CD, ее уравнение y=ax+b. Возьмем на CD точки, обозначим их со штрихами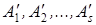 
- имеющие с точками A 1, A 2,…, As одинаковые абсциссы. Согласно метода наименьших квадратов, найдем сумму квадратов разностей ординат соответствующих точкам
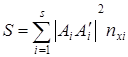
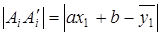
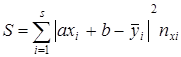
Следовательно, S - сумма двух независимых переменных a и b. Для искомой прямой сумма минимальна, используя необходимые условия экстремумов функций, т.е обращение в 0 ее первых частных производных.
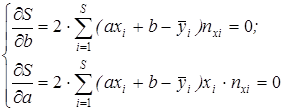
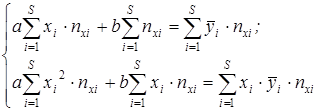(1)
;
.
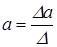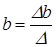Разделим оба уравнения на объем совокупности n:
;
;
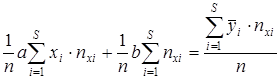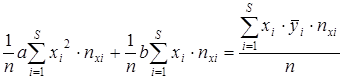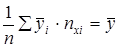-общая средняя;
.
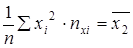Возьмем слагаемое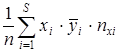 
, вместо 
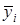подставим сумму 
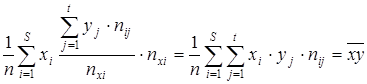-это есть средняя арифметическая переменных 
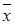и 
.
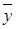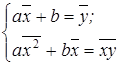(2)
Из 1-го уравнения выразим b;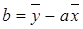 
И подставим b:
;
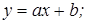
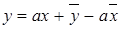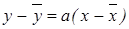(3)
Это уравнение- это прямая регрессии y на x проходит через точку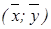 
. Причем точка 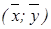- это средняя точка корреляционного графика, коэффициент в уравнении прямой регрессии называется коэффициентом регрессии y на x и обозначается как 
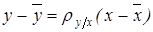(4).
Найдем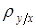 
из системы (2).
Подставим 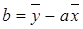во 2-ое уравнение:
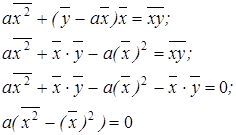
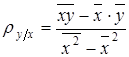(5)
Знаменатель - это дисперсия переменной x относительно ее общей средней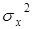 
.
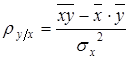(6)
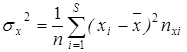
Аналогично можно составит уравнение прямой регрессии x на y. Для этого в прямоугольной плоскости координат отмечают точки Cj с координатами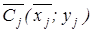 
. Проводя аналогичные рассуждения мы получаем формулы для параметров c и d для уравнения x=cy+d, и уравнение искомой прямой регрессии x на y запишется в виде
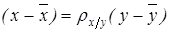(7)
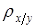-называется коэффициентом регрессии x на y и определяется также по формуле (5)
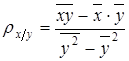или 
;
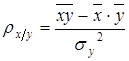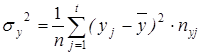(8)
Отметим свойства коэффициентов регрессии.
1. Коэффициенты регрессии y на x и x на y имеют одинаковые знаки. Знаменатель всегда положительный, поэтому эти знаки определяются числителями.
2. Коэффициент регрессии y на x является условным коэффициентом прямой регрессии y на x, а коэффициент регрессии x на y величиной обратной угловому коэффициенту прямой регрессии x на y, из уравнений (4) и (7).
