Серийная выборка

Сущность серийной выборки заключается в том, что вместо случайного отбора единиц совокупности осуществляется отбор групп (серий, гнезд). Внутри отобранных серий производится сплошное наблюдение. Единицей отбора при этом является группа или серия, а не отдельная единица генеральной совокупности, как это имело место в рассматриваемых ранее выборках. Отбор серий может производиться в порядке повторного и бесповторного отбора. Серии могут быть равновеликими и неравновеликими.

На практике чаще применяют отбор с равными сериями. Данный способ отбора удобен в тех случаях, когда единицы генеральной совокупности изначально объединены в небольшие группы или серии. В качестве таких серий могут выступать упаковки с готовой продукцией, партии товара, бригады и др.

Таблица 3 – Формулы ошибок серийной выборки

	Способ отбора серий
повторный	бесповторный
Средняя ошибка для средней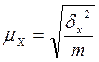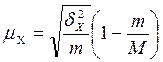
Средняя ошибка для доли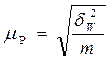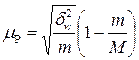

В таблице 3 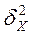- межгрупповая выборочная дисперсия

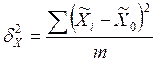
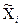- средний уровень признака в серии

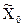- средний уровень признака для всей выборки

m – Число серий в выборке

М – число серий в генеральной совокупности

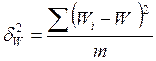
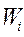- доля единиц, обладающих данным признаком в серии

W – доля единиц, обладающих данным признаком во всей выборочной совокупности

Ошибка серийной выборки больше, чем при любом другом способе отбора. Тем не менее серийный отбор широко применяется на практике благодаря более легкой по сравнению с другими способами организацией.

Приведем пример расчетов при серийном отборе.

При контрольной проверке качества апельсинов проведена 10%-ая серийная выборка. Из партии содержащий 50 ящиков апельсинов (вес ящиков одинаков), методом механического отбора взято 5 ящиков. В результате сплошного обследования находящихся в ящиках апельсинов получили данные об удельном весе испортившихся апельсинов в каждом ящике, попавшем в выборку. Результаты следующие:

Требуется с вероятностью 0,95 установить доверительные интервалы удельного веса испортившихся апельсинов для всей партии (50 ящиков).

Решение:

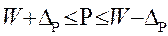
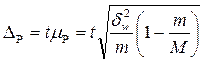
При p=0,95 t = 1,96 (см. таблицу функции Лапласа)

W=(1,2 + 1,8 + 2 + 1 + 1,5): 5=1,5% или 0,015

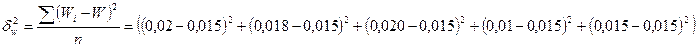: 5= 0,0000136

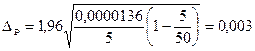или 0,3%

1,5 – 0,3≤P≤ 1,5 + 0,3

1,2% ≤ P ≤ 1,8%

Итак, с вероятностью 0,95 можно утверждать, что удельный вес испортившихся апельсинов во всей партии продукции будет находиться в пределах от 1,2 % до 1,8 %.